题目内容
在平行四边形中,∠ADC的邻补角的平分线交BC的延长线于E,延长ED交BA的延长线于F,试判断△FBE的形状并说明理由.
考点:平行四边形的性质
专题:
分析:利用平行四边形的性质以及平行线的性质和角平分线的性质得出∠E=∠F,进而得出答案.
解答: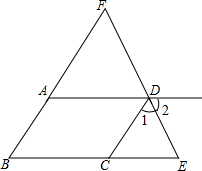 解:△FBE是等腰三角形,
解:△FBE是等腰三角形,
理由:如图所示:
∵四边形ABCD是平行四边形,
∴AB∥DC,AD∥BC,
∴∠2=∠E,
∵∠1=∠2,
∴∠1=∠E,
∵AB∥DC,
∴∠1=∠F,
∴∠E=∠F,
∴△FBE是等腰三角形.
 解:△FBE是等腰三角形,
解:△FBE是等腰三角形,理由:如图所示:
∵四边形ABCD是平行四边形,
∴AB∥DC,AD∥BC,
∴∠2=∠E,
∵∠1=∠2,
∴∠1=∠E,
∵AB∥DC,
∴∠1=∠F,
∴∠E=∠F,
∴△FBE是等腰三角形.
点评:此题主要考查了平行四边形的性质以及角平分线的性质,得出∠1=∠E是解题关键.

练习册系列答案
相关题目
李红同学遇到了这样一道题:tan(α+10°)=1,你猜想锐角α的度数应是( )
| A、20° | B、35° |
| C、45° | D、50° |
下列等式正确的是( )
| A、(2x)3=2x3 |
| B、a2•a3=a6 |
| C、π6÷π3=π2 |
| D、x9÷x5=x4 |
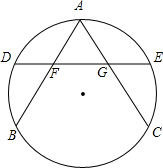 如图,A、B、C是圆O上的三点,连接
如图,A、B、C是圆O上的三点,连接
 如图,在△ABC中,∠ACB=3∠B,∠1=∠2,CD⊥AD于D,求证:AB-AC=2CD.
如图,在△ABC中,∠ACB=3∠B,∠1=∠2,CD⊥AD于D,求证:AB-AC=2CD.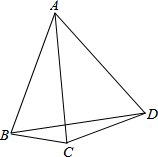 如图所示,AB=AC=AD,∠DBC=18°,则∠CAD=
如图所示,AB=AC=AD,∠DBC=18°,则∠CAD=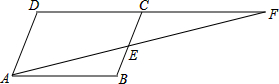 如图,?ABCD中,E为BC中点,连接AE交DC的延长线于F,求证:AE=EF.
如图,?ABCD中,E为BC中点,连接AE交DC的延长线于F,求证:AE=EF.