题目内容
 如图,在△ABC中,∠ACB=3∠B,∠1=∠2,CD⊥AD于D,求证:AB-AC=2CD.
如图,在△ABC中,∠ACB=3∠B,∠1=∠2,CD⊥AD于D,求证:AB-AC=2CD.考点:等腰三角形的判定与性质
专题:证明题
分析:延长CD交AB于点E,可知△ACE为等腰三角形,可知AE=AC,可知AB-AC=BE,再由∠ACB=3∠B,可得出BE=EC,可得出结论.
解答: 证明:延长CD交AB于E,
证明:延长CD交AB于E,
∵∠1=∠2,∠ADE=∠ADC,
∴∠AED=∠ACD,
∴AE=AC,
∴ED=CD,
∴EB=EC,
∵∠ACD=∠ACB-∠ECB=3∠B-∠ECB,
∠AED=∠B+∠ECB,
∴3∠B-∠ECB=∠B+∠ECB,
∴∠B=∠ECB,
∴EB=EC,
∵EB=AB-AE=AB-AC,
EC=2CD,
∴AB-AC=2CD.
 证明:延长CD交AB于E,
证明:延长CD交AB于E,∵∠1=∠2,∠ADE=∠ADC,
∴∠AED=∠ACD,
∴AE=AC,
∴ED=CD,
∴EB=EC,
∵∠ACD=∠ACB-∠ECB=3∠B-∠ECB,
∠AED=∠B+∠ECB,
∴3∠B-∠ECB=∠B+∠ECB,
∴∠B=∠ECB,
∴EB=EC,
∵EB=AB-AE=AB-AC,
EC=2CD,
∴AB-AC=2CD.
点评:本题主要考查等腰三角形的性质和判定,由条件证得BE=CE是解题的关键.

练习册系列答案
相关题目
下面的图形中是正方体的展开图的是( )
A、 |
B、 |
C、 |
D、 |
下列式子是分式的是( )
A、2x2+
| ||
B、
| ||
C、
| ||
D、
|
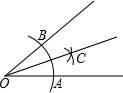 如图,用直尺和圆规作一个角的平分线,是运用了“全等三角形的对应角相等”这一性质,由作图所得条件,判定三角形全等运用的方法是( )
如图,用直尺和圆规作一个角的平分线,是运用了“全等三角形的对应角相等”这一性质,由作图所得条件,判定三角形全等运用的方法是( )| A、SAS | B、ASA |
| C、AAS | D、SSS |
点P(-3,5)关于x轴的对称点P′的坐标是( )
| A、(3,5) |
| B、(5,-3) |
| C、(3,-5) |
| D、(-3,-5) |
a、b为任何非零有理数,则
+
+
的可能取值是( )
| a |
| |a| |
| b |
| |b| |
| ab |
| |ab| |
| A、-3或1 | B、3或1或-1 |
| C、1或3 | D、-1或3 |