题目内容
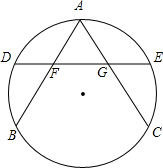 如图,A、B、C是圆O上的三点,连接
如图,A、B、C是圆O上的三点,连接 |
| AB |
 |
| AC |
考点:圆心角、弧、弦的关系
专题:
分析:连接OD和OE交AB于M点,交AC于N点,根据D为
的中点,E为
的中点可知OD⊥AB,OE⊥AC.再由OD=OE可知∠ODE=∠OED,故可得出∠AFE=∠AGF,由此可得出结论.
 |
| AB |
 |
| AC |
解答: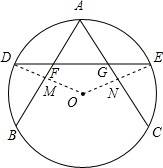 解:AF=AG.
解:AF=AG.
理由:连接OD和OE交AB于M点,交AC于N点,
∵D为
的中点,OD过圆心O点
∴OD⊥AB.
同理OE⊥AC.
∵OD=OE,
∴∠ODE=∠OED,
∴90°-∠ODE=90°-∠OED,即∠DFM=∠EGN.
∵∠DFM=∠AFE,∠EGN=∠AGF,
∴∠AFE=∠AGF,
∴AF=AG.
 解:AF=AG.
解:AF=AG.理由:连接OD和OE交AB于M点,交AC于N点,
∵D为
 |
| AB |
∴OD⊥AB.
同理OE⊥AC.
∵OD=OE,
∴∠ODE=∠OED,
∴90°-∠ODE=90°-∠OED,即∠DFM=∠EGN.
∵∠DFM=∠AFE,∠EGN=∠AGF,
∴∠AFE=∠AGF,
∴AF=AG.
点评:本题考查的是圆心角、弧、弦的关系,根据题意作出辅助线,构造出等腰三角形是解答此题的关键.

练习册系列答案
相关题目
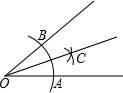 如图,用直尺和圆规作一个角的平分线,是运用了“全等三角形的对应角相等”这一性质,由作图所得条件,判定三角形全等运用的方法是( )
如图,用直尺和圆规作一个角的平分线,是运用了“全等三角形的对应角相等”这一性质,由作图所得条件,判定三角形全等运用的方法是( )| A、SAS | B、ASA |
| C、AAS | D、SSS |
下列命题中
①平分弦的直径垂直于弦;②二次函数y=x2+bx-2 与x轴有两个交点;③如果两条弧相等那么它们所对的弦相等;④有一个角是80°的两个等腰三角形相似;
真命题有( )个.
①平分弦的直径垂直于弦;②二次函数y=x2+bx-2 与x轴有两个交点;③如果两条弧相等那么它们所对的弦相等;④有一个角是80°的两个等腰三角形相似;
真命题有( )个.
| A、1 | B、2 | C、3 | D、4 |
在有理数中( )
| A、有最大的数,也有最小的数 |
| B、有最大的数,但没有最小的数 |
| C、有最小的数,但没有最大的数 |
| D、既没有最大的数,也没有最小的数 |
 如图,在Rt△ABC和Rt△BAD中,CE=DE,∠C=∠D=90°.
如图,在Rt△ABC和Rt△BAD中,CE=DE,∠C=∠D=90°. 如图,已知AB是⊙O的直径,BC为弦,∠ABC=40°,点D为
如图,已知AB是⊙O的直径,BC为弦,∠ABC=40°,点D为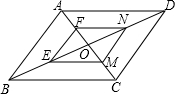 如图,在?ABCD中,AC与BD交于点O,点F,E,M,N分别是AO,BO,CO,DO的中点,这样形成一个?FEMN,你能证明?ABCD∽?FEMN吗?
如图,在?ABCD中,AC与BD交于点O,点F,E,M,N分别是AO,BO,CO,DO的中点,这样形成一个?FEMN,你能证明?ABCD∽?FEMN吗?