题目内容
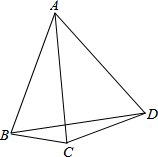 如图所示,AB=AC=AD,∠DBC=18°,则∠CAD=
如图所示,AB=AC=AD,∠DBC=18°,则∠CAD=考点:圆周角定理
专题:
分析:先根据AB=AC=AD得出B、C、D三点在以点A为圆心,以AB为半径的圆上,再根据圆周角定理即可得出结论.
解答:解:∵AB=AC=AD,
∴B、C、D三点在以点A为圆心,以AB为半径的圆上.
∵∠DBC=18°,
∴∠CAD=2∠DBC=36°.
故答案为:36°.
∴B、C、D三点在以点A为圆心,以AB为半径的圆上.
∵∠DBC=18°,
∴∠CAD=2∠DBC=36°.
故答案为:36°.
点评:本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
将一直角三角形的三边长变为原来的2.5倍后,得到的三角形是( )
| A、锐角三角形 | B、钝角三角形 |
| C、直角三角形 | D、无法确定 |
下列计算错误的是( )
A、
| ||||||
B、3
| ||||||
C、
| ||||||
D、当x<1时,
|
下列命题中
①平分弦的直径垂直于弦;②二次函数y=x2+bx-2 与x轴有两个交点;③如果两条弧相等那么它们所对的弦相等;④有一个角是80°的两个等腰三角形相似;
真命题有( )个.
①平分弦的直径垂直于弦;②二次函数y=x2+bx-2 与x轴有两个交点;③如果两条弧相等那么它们所对的弦相等;④有一个角是80°的两个等腰三角形相似;
真命题有( )个.
| A、1 | B、2 | C、3 | D、4 |
下列合并同类项正确的是( )
| A、2x+x=2x2 |
| B、2x+x=3x |
| C、5a2-3a2=2 |
| D、2x+3y=5xy |
若△ABC≌△DEF,且△ABC的周长为22,AB=5,BC=8,则DF的长为( )
| A、5 | B、8 | C、9 | D、5或8 |
 如图,已知AB是⊙O的直径,BC为弦,∠ABC=40°,点D为
如图,已知AB是⊙O的直径,BC为弦,∠ABC=40°,点D为
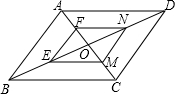 如图,在?ABCD中,AC与BD交于点O,点F,E,M,N分别是AO,BO,CO,DO的中点,这样形成一个?FEMN,你能证明?ABCD∽?FEMN吗?
如图,在?ABCD中,AC与BD交于点O,点F,E,M,N分别是AO,BO,CO,DO的中点,这样形成一个?FEMN,你能证明?ABCD∽?FEMN吗?