题目内容
16.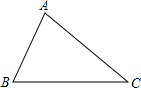 如图,已知△ABC,按下列语句要求用尺规作图(保留作图痕迹,不写作法);
如图,已知△ABC,按下列语句要求用尺规作图(保留作图痕迹,不写作法);(1)作出BC的垂直平分线DE,垂足为D,交AC于点E;
(2)作出∠ACB的角平分线CF,交AB于点F;
(3)在BC上找出一点P,使△PEF的周长最小.
分析 (1)利用线段垂直平分线的作法得出BC的垂直平分线即可;
(2)利用角平分线的作法得出即可;
(3)由于△PEF的周长=PF+PE+EF,而EF是定值,故只需在BC上找一点P,使PF+PE最小,作出F关于BC的对称点为F′,连接EF′得出即可.
解答  解:(1)如图所示:DE即为所求;
解:(1)如图所示:DE即为所求;
(2)如图所示:CF即为所求;
(3)如图所示:P点即为所求.
点评 本题考查了角平分线的作法以及线段垂直垂直分线的作法以及轴对称中最短路线问题,解这类问题的关键是把两条线段的和转化为一条线段,运用三角形三边关系解决.

练习册系列答案
相关题目
11.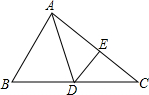 如图,AD是△ABC的中线,DE是△ADC的高线,AB=3,AC=5,DE=2,那么点D到AB的距离是( )
如图,AD是△ABC的中线,DE是△ADC的高线,AB=3,AC=5,DE=2,那么点D到AB的距离是( )
 如图,AD是△ABC的中线,DE是△ADC的高线,AB=3,AC=5,DE=2,那么点D到AB的距离是( )
如图,AD是△ABC的中线,DE是△ADC的高线,AB=3,AC=5,DE=2,那么点D到AB的距离是( )| A. | $\frac{10}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{6}{5}$ | D. | 2 |
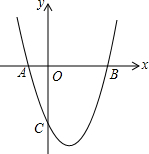 如图,抛物线y=x2+bx+c与x轴交于A(-1,0)、B(3,0)两点.
如图,抛物线y=x2+bx+c与x轴交于A(-1,0)、B(3,0)两点.