题目内容
6.已知E是圆内接四边形ABCD的边CD的延长线上一点,I是△ABC的内心,若∠ABC=70°,∠ACB=60°,DE=DA,则∠DEI的度数是25°.分析 连接AI、CI.在△ABC中,由三角形的内角和定理可知:∠BAC=50°,因为⊙I是△ABC的内切圆,所以∠1=$\frac{1}{2}∠ACB=30°$,∠2=$\frac{1}{2}∠CAB=25°$,由圆内接四边形的性质可知∠EDA=70°,由等腰三角形的性质可知∠DEA=55°,然后可证明∠DEA+∠AIC=180°,故点E、A、I、C共圆,所以∠DEI=25°.
解答 解:如图所示: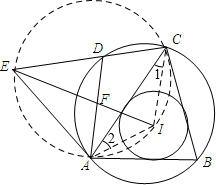
解:连接AI、CI.
在△ABC中,∠BAC=180°-∠ABC-∠ACB=180°-70°-60°=50°,
∵⊙I是△ABC的内切圆,
∴∠1=$\frac{1}{2}∠ACB=30°$,∠2=$\frac{1}{2}∠CAB=25°$.
∵四边形ABCD是圆内接四边形,
∴∠EDA=∠B=70°.
∵DE=DA,
∴∠DEA=∠DAE=$\frac{1}{2}×(180°-70°)$=55°.
在△ACI中,∠AIC=180°-∠1-∠2=125°.
∴∠DEA+∠AIC=180°.
∴点E、A、I、C共圆.
∴∠DEI=∠2=25°.
故答案为:25°.
点评 本题主要考查的是三角形的内切圆、圆内接四边形的性质和判定、等腰三角形的性质、三角形的内角和定理,证得点E、A、I、C共圆是解题的关键.

练习册系列答案
相关题目
17.下列条件中,不能判定四边形是平行四边形的是( )
| A. | 两组对边分别平行 | B. | 一组对边平行,另一组对边相等 | ||
| C. | 两组对边分别相等 | D. | 一组对边平行且相等 |
18.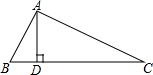 如图:在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,BD=1,AC=$2\sqrt{5}$,则AD等于( )
如图:在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,BD=1,AC=$2\sqrt{5}$,则AD等于( )
 如图:在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,BD=1,AC=$2\sqrt{5}$,则AD等于( )
如图:在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,BD=1,AC=$2\sqrt{5}$,则AD等于( )| A. | 1 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 2 | D. | 3 |
 在矩形ABCD中,M是AD边上的中点,N是DC边上的中点,AN与MC交于点P,若∠MCB=∠NBC+33°,则∠MPA=33°.
在矩形ABCD中,M是AD边上的中点,N是DC边上的中点,AN与MC交于点P,若∠MCB=∠NBC+33°,则∠MPA=33°.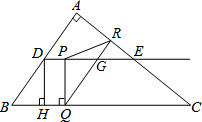 如图,在Rt△ABC中,∠A=90°,AB=6cm,AC=8cm,D,E分别是边AB,AC的中点,点P从点D出发沿DE方向以1cm/s的速度运动,过点P作PQ⊥BC于Q,过点Q作QR∥BA交AC于R,交DE于G,当点Q与点C重合时,点P停止运动.设点P运动时间为ts.
如图,在Rt△ABC中,∠A=90°,AB=6cm,AC=8cm,D,E分别是边AB,AC的中点,点P从点D出发沿DE方向以1cm/s的速度运动,过点P作PQ⊥BC于Q,过点Q作QR∥BA交AC于R,交DE于G,当点Q与点C重合时,点P停止运动.设点P运动时间为ts.