题目内容
(1)如图1,角∠MON=84°,点A、B分别在射线OM、ON上移动,△AOB的角平分线AC与BD交于点P.试问:随着点A、B位置的变化,∠APB的大小是否会变化?若保持不变,请求出∠APB的度数.若发生变化,请说明理由.
(2)如图2,两条互相垂直的直线MN、PQ,垂足为O,OE是∠PON的角平分线,点A、B分别在射线OE、OP上移动,BD是∠ABP的平分线,BD的反向延长线交∠OAB的平分线于点P,随着点A、B位置的变化,此时∠APB的大小是否会变化?若保持不变,请求出∠APB的度数.若发生变化,请说明理由.
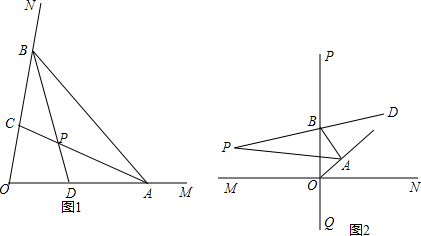
(2)如图2,两条互相垂直的直线MN、PQ,垂足为O,OE是∠PON的角平分线,点A、B分别在射线OE、OP上移动,BD是∠ABP的平分线,BD的反向延长线交∠OAB的平分线于点P,随着点A、B位置的变化,此时∠APB的大小是否会变化?若保持不变,请求出∠APB的度数.若发生变化,请说明理由.

考点:三角形内角和定理,角平分线的定义,三角形的外角性质
专题:
分析:(1)先根据三角形内角和定理求出∠OAB+∠OBA的度数,再由角平分线的定义得出∠PAB+∠PBA的度数,在△PAB中根据三角形内角和定理即可得出结论;
(2)先根据MN⊥PQ,且OE平分∠PON得出∠BOA的度数,再根据OE是∠PON的角平分线,BD是∠ABP的平分线即可得出结论.
(2)先根据MN⊥PQ,且OE平分∠PON得出∠BOA的度数,再根据OE是∠PON的角平分线,BD是∠ABP的平分线即可得出结论.
解答:解:(1)∠APB的大小不变,始终为132°.
∵在△OAB中,
∵∠MON=84°,
∴∠OAB+∠OBA=180°-∠MON=96°.
∵△AOB的角平分线AC与BD交于点P,
∴∠PAB+∠PBA=
(∠OAB+∠OBA)=48°
∴在△PAB中,∠APB=180°-(∠PAB+∠PBA)=132°;
(2)∠APB的大小不变,始终为22.5°.
∵MN⊥PQ,且OE平分∠PON,
∴∠BOA=45°,
∴∠PBA-∠BAO=∠BOA=45°,
∵OE是∠PON的角平分线,BD是∠ABP的平分线,
∴
∠PBA-
∠BAO=
∠BOA=22.5°
∴∠APB=∠DBA-∠PAB=
∠PBA-
∠BAO=22.5°.
∵在△OAB中,
∵∠MON=84°,
∴∠OAB+∠OBA=180°-∠MON=96°.
∵△AOB的角平分线AC与BD交于点P,
∴∠PAB+∠PBA=
| 1 |
| 2 |
∴在△PAB中,∠APB=180°-(∠PAB+∠PBA)=132°;
(2)∠APB的大小不变,始终为22.5°.
∵MN⊥PQ,且OE平分∠PON,
∴∠BOA=45°,
∴∠PBA-∠BAO=∠BOA=45°,
∵OE是∠PON的角平分线,BD是∠ABP的平分线,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠APB=∠DBA-∠PAB=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查的是三角形内角和定理及角平分线的性质,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
相关题目
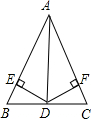 如图,在△ABC中,点D是BC的中点,DE⊥AB,DF⊥AC,E,F为垂足,DE=DF,求证:BE=CF.
如图,在△ABC中,点D是BC的中点,DE⊥AB,DF⊥AC,E,F为垂足,DE=DF,求证:BE=CF.