题目内容
12.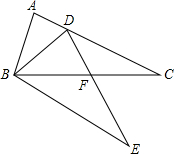 如图,在△ABC中,AC=BC,点D在边AC上,AB=BD,BE=ED,且∠CBE=∠ABD,DE与CB交于点F.求证:
如图,在△ABC中,AC=BC,点D在边AC上,AB=BD,BE=ED,且∠CBE=∠ABD,DE与CB交于点F.求证:(1)BD2=AD•BE;
(2)CD•BF=BC•DF.
分析 (1)由∠CBE=∠ABD,得到∠ABC=∠DBE等量代换得到∠A=∠DBE,根据等腰三角形的性质得到∠A=∠ADB,∠DBE=∠BDE,等量代换得到∠A=∠DBE=∠BDE,推出△ABD∽△DEB,根据相似三角形的性质即可得到结论;
(2)通过△ABC≌△DBE,根据全等三角形的性质得到∠C=∠E,BE=BC,由于∠CFD=∠EFB,证得△CFD∽△EFB,根据相似三角形的性质得到结论.
解答 证明:(1)∵∠CBE=∠ABD,
∴∠ABC=∠DBE,
∵∠A=∠ABC,
∴∠A=∠DBE,
∵AB=BD,
∴∠A=∠ADB,
∵BE=DE,
∴∠DBE=∠BDE,
∴∠A=∠DBE=∠BDE,
∴△ABD∽△DEB,
∴$\frac{AD}{BD}=\frac{BD}{BE}$,
即BD2=AD•BE;
(2)在△ABC与△DBE中,
$\left\{\begin{array}{l}{∠A=∠BDE}\\{AB=DB}\\{∠ABC=∠DBE}\end{array}\right.$,
∴△ABC≌△DBE,
∴∠C=∠E,BE=BC,
∵∠CFD=∠EFB,
∴△CFD∽△EFB,
∴$\frac{BF}{DF}=\frac{BE}{CD}$,
∴$\frac{BF}{DF}=\frac{BC}{CD}$,
即:CD•BF=BC•DF.
点评 本题考查了相似三角形的判定和性质,等腰三角形的性质,全等三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
7.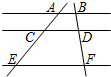 如图,如果AB∥CD∥EF,那么下列结论正确的是( )
如图,如果AB∥CD∥EF,那么下列结论正确的是( )
 如图,如果AB∥CD∥EF,那么下列结论正确的是( )
如图,如果AB∥CD∥EF,那么下列结论正确的是( )| A. | $\frac{AC}{AE}$=$\frac{CD}{EF}$ | B. | $\frac{AC}{BD}$=$\frac{CE}{DF}$ | C. | $\frac{AC}{CE}$=$\frac{AB}{CD}$ | D. | $\frac{AC}{DF}$=$\frac{BD}{CE}$ |
1.下列等式正确的是( )
| A. | -|3|=|-3| | B. | |3|=|-3| | C. | |-3|=-3 | D. | -(-3)=-|-3| |
 如图,∠C=∠1,∠2与∠D互余,BE⊥DF,垂足为G.求证:AB∥CD.
如图,∠C=∠1,∠2与∠D互余,BE⊥DF,垂足为G.求证:AB∥CD. 如图,一次函数y=-x+2与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,点A的横坐标为-2.
如图,一次函数y=-x+2与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,点A的横坐标为-2.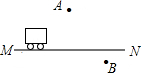 如图所示,一辆汽车在平直的公路上由M向N方向行驶,A、B分别是位于公路MN两侧的村庄.
如图所示,一辆汽车在平直的公路上由M向N方向行驶,A、B分别是位于公路MN两侧的村庄.