题目内容
12.绍兴是著名的桥乡,如图,圆拱桥的拱顶到水面的距离CD=8m,桥拱半径OC=5m,则水面宽AB=( )
| A. | 4 m | B. | 5 m | C. | 6 m | D. | 8 m |
分析 连接OA,根据勾股定理求出AD的长,根据垂径定理计算即可.
解答 解: 连接OA,
连接OA,
∵CD=8m,OC=5m,
∴OD=3m,
∴AD=$\sqrt{O{A}^{2}-O{D}^{2}}$=4m,
由垂径定理得,AB=2AD=8m,
故选:D.
点评 本题考查的是垂径定理和勾股定理的应用,掌握垂直于弦的直径平分弦且平分弦所对的弧是解题的关键.

练习册系列答案
相关题目
20.将直角三角形的各边都缩小或扩大同样的倍数后,得到的三角形( )
| A. | 可能是锐角三角形 | B. | 不可能是直角三角形 | ||
| C. | 仍然是直角三角形 | D. | 可能是钝角三角形 |
7. 在一个可以改变容积的密闭容器内,装有一定质量m的某种气体,当改变容积V时,气体的密度p也随之改变,ρ与V在一定范围内满足ρ=$\frac{m}{v}$,它的图象如图所示,则该气体的质量m为( )
在一个可以改变容积的密闭容器内,装有一定质量m的某种气体,当改变容积V时,气体的密度p也随之改变,ρ与V在一定范围内满足ρ=$\frac{m}{v}$,它的图象如图所示,则该气体的质量m为( )
 在一个可以改变容积的密闭容器内,装有一定质量m的某种气体,当改变容积V时,气体的密度p也随之改变,ρ与V在一定范围内满足ρ=$\frac{m}{v}$,它的图象如图所示,则该气体的质量m为( )
在一个可以改变容积的密闭容器内,装有一定质量m的某种气体,当改变容积V时,气体的密度p也随之改变,ρ与V在一定范围内满足ρ=$\frac{m}{v}$,它的图象如图所示,则该气体的质量m为( )| A. | 1.4kg | B. | 5kg | C. | 7kg | D. | 6.4kg |
17.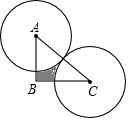 如图,在Rt△ABC中,∠ABC=90°,AB=6cm,BC=8cm,分别以$\frac{1}{2}$AC的长为半径作圆,将Rt△ABC截去两个扇形,则余下阴影部分的面积为( )cm2.
如图,在Rt△ABC中,∠ABC=90°,AB=6cm,BC=8cm,分别以$\frac{1}{2}$AC的长为半径作圆,将Rt△ABC截去两个扇形,则余下阴影部分的面积为( )cm2.
 如图,在Rt△ABC中,∠ABC=90°,AB=6cm,BC=8cm,分别以$\frac{1}{2}$AC的长为半径作圆,将Rt△ABC截去两个扇形,则余下阴影部分的面积为( )cm2.
如图,在Rt△ABC中,∠ABC=90°,AB=6cm,BC=8cm,分别以$\frac{1}{2}$AC的长为半径作圆,将Rt△ABC截去两个扇形,则余下阴影部分的面积为( )cm2.| A. | $\frac{25}{4}$P | B. | 24-$\frac{5}{4}$P | C. | 24-$\frac{25}{6}$P | D. | 24-$\frac{25}{4}$P |
4.关于x的方程6x-5m=2的解是x=m,则m的值是( )
| A. | 2 | B. | -2 | C. | $\frac{2}{11}$ | D. | $-\frac{2}{11}$ |
2.下面计算正确的是( )
| A. | 6b-5b=1 | B. | 2m+3m2=5m3 | C. | -(c-d)=-c+d | D. | 2(a-b)=2a-b |
 如图,在四边形ABCD中,对角线AC⊥BD,且AC=8,BD=10,E,F分别是边AB,CD的中点,则EF=$\sqrt{41}$.
如图,在四边形ABCD中,对角线AC⊥BD,且AC=8,BD=10,E,F分别是边AB,CD的中点,则EF=$\sqrt{41}$.


