题目内容
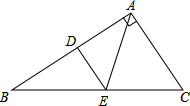 如图,在直角△ABC中,∠BAC=90°,AB=8,AC=6,DE是AB边的垂直平分线,垂足为D,交边BC于点E,连接AE,则△ACE的周长为
如图,在直角△ABC中,∠BAC=90°,AB=8,AC=6,DE是AB边的垂直平分线,垂足为D,交边BC于点E,连接AE,则△ACE的周长为考点:线段垂直平分线的性质,勾股定理
专题:几何图形问题,数形结合,转化思想
分析:由DE是AB边的垂直平分线,可得AE=BE,又由在直角△ABC中,∠BAC=90°,AB=8,AC=6,利用勾股定理即可求得BC的长,继而由△ACE的周长=AC+BC,求得答案.
解答:解:∵DE是AB边的垂直平分线,
∴AE=BE,
∵在直角△ABC中,∠BAC=90°,AB=8,AC=6,
∴BC=
=10,
∴△ACE的周长为:AC+AE+CE=AC+BE+CE=AC+BC=6+10=16.
故答案为:16.
∴AE=BE,
∵在直角△ABC中,∠BAC=90°,AB=8,AC=6,
∴BC=
| AB2+AC2 |
∴△ACE的周长为:AC+AE+CE=AC+BE+CE=AC+BC=6+10=16.
故答案为:16.
点评:此题考查了线段垂直平分线的性质以及勾股定理.此题难度不大,注意掌握数形结合思想与转化思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 如图,将三角形ABC向左平移2个单位长度,再向上平移3个单位长度.
如图,将三角形ABC向左平移2个单位长度,再向上平移3个单位长度. 如图,在四边形ABCD中,AD∥BC,且AD=BC,若再补充一个条件,如∠A=
如图,在四边形ABCD中,AD∥BC,且AD=BC,若再补充一个条件,如∠A=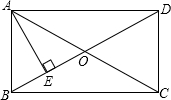 如图,在矩形ABCD中,AE⊥BD于E,BE:ED=1:3,AB=4cm,则AC=
如图,在矩形ABCD中,AE⊥BD于E,BE:ED=1:3,AB=4cm,则AC= 如图,以点O为圆心,OB为半径画弧,交数轴于点A,若点A所表示的数为x,则x2-1的立方根为
如图,以点O为圆心,OB为半径画弧,交数轴于点A,若点A所表示的数为x,则x2-1的立方根为 某班有54人.其中参加读书活动的人数为18人,参加科技活动人数占全班人数的
某班有54人.其中参加读书活动的人数为18人,参加科技活动人数占全班人数的 如图,已知直线a∥b,∠l=43°,则∠2的度数为
如图,已知直线a∥b,∠l=43°,则∠2的度数为