题目内容
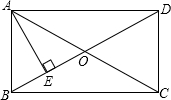如图，在矩形ABCD中，AE⊥BD于E，BE：ED=1：3，AB=4cm，则AC=考点：矩形的性质
专题：几何图形问题
分析：由在矩形ABCD中，AE⊥BD于E，BE：ED=1：3，易证得△OAB是等边三角形，则可求得AC的长．
解答：解：∵四边形ABCD是矩形，
∴OB=OD，OA=OC，AC=BD，
∴OA=OB，
∵BE：ED=1：3，
∴BE：BD=1：4，
∴BE：OB=1：2，
即BE=OE，
∵AE⊥BD，
∴AB=OA，
∴OA=OB=AB=4cm，
∴AC=2OA=8（cm）．
故答案为：8cm．
∴OB=OD，OA=OC，AC=BD，
∴OA=OB，
∵BE：ED=1：3，
∴BE：BD=1：4，
∴BE：OB=1：2，
即BE=OE，
∵AE⊥BD，
∴AB=OA，
∴OA=OB=AB=4cm，
∴AC=2OA=8（cm）．
故答案为：8cm．
点评：此题考查了矩形的性质、线段垂直平分线的性质以及等边三角形的判定与性质．此题难度适中，注意掌握数形结合思想的应用．
练习册系列答案
智能训练练测考系列答案
相关题目
如图所示，直线a，b被直线c所截，若∠2=∠3，∠4=120°．
如图，G、E、H、F分别是?ABCD的边AD、AB、BC、CD上的点，且EF∥BC，GH∥AB，则图中不包括?ABCD的平行四边形有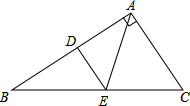
如图，在直角△ABC中，∠BAC=90°，AB=8，AC=6，DE是AB边的垂直平分线，垂足为D，交边BC于点E，连接AE，则△ACE的周长为
如图，已知AB∥CD，∠C=30°，∠B=150°，则∠1=
如图所示，当剪子口∠AOB减少10°时，∠COD也
如图所示，∠1与∠3是直线