题目内容
在△ABC中,∠ACB=90°,AC=8cm,BC=6cm,分別以AC、BC为边作正方形AEDC、BCFG,则△BEF的面积是 cm2.
考点:勾股定理
专题:几何图形问题
分析:连接EC并延长交BF于点H,先根据全等三角形的判定定理得出△ABC≌△DFC,故可得出DF=AB,∠CDF=∠CAB,进而可得出∠EDF=∠EAB,再由SAS定理可得出△EDF≌△EAB,故EF=EB,再根据CF=CB可知EH是BF的垂直平分线,根据勾股定理可得出CE、BF及CH的长,由三角形的面积公式即可得出结论.
解答: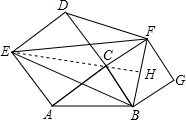 解:连接EC并延长交BF于点H,
解:连接EC并延长交BF于点H,
∵四边形AEDC、BCFG均是正方形,
∴∠DCA=∠BCF=90°,
∵∠ACB=90°,
∴∠DCF=90°,
在△ABC与△DFC中,
,
∴△ABC≌△DFC(SAS),
∴DF=AB,∠CDF=∠CAB,
∴∠EDF=∠EAB,
在△EDF与△EAB中,
,
∴△EDF≌△EAB(SAS),
∴EF=EB,
∴△BEF是等腰三角形,
∵CF=CB,
∴△BCF是等腰三角形,
∴EH是BF的垂直平分线,
∵AC=8cm,BC=6cm,
∴CE=
=8
cm,BF=
=6
cm,
∴CH=
BF=3
cm,
∴BH=CE+CH=8
+3
=11
cm,
∴S△BEF=
BF•EH=
×6
×11
=66cm2.
故答案为:66.
 解:连接EC并延长交BF于点H,
解:连接EC并延长交BF于点H,∵四边形AEDC、BCFG均是正方形,
∴∠DCA=∠BCF=90°,
∵∠ACB=90°,
∴∠DCF=90°,
在△ABC与△DFC中,
|
∴△ABC≌△DFC(SAS),
∴DF=AB,∠CDF=∠CAB,
∴∠EDF=∠EAB,
在△EDF与△EAB中,
|
∴△EDF≌△EAB(SAS),
∴EF=EB,
∴△BEF是等腰三角形,
∵CF=CB,
∴△BCF是等腰三角形,
∴EH是BF的垂直平分线,
∵AC=8cm,BC=6cm,
∴CE=
| 82+82 |
| 2 |
| 62+62 |
| 2 |
∴CH=
| 1 |
| 2 |
| 2 |
∴BH=CE+CH=8
| 2 |
| 2 |
| 2 |
∴S△BEF=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
故答案为:66.
点评:本题考查正的勾股定理,方形的性质,三角形的面积等知识点,先根据题意判断出△BEF与△BCF是等腰三角形是解答此题的关键.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 如图,2台大收割机和5台小收割机均工作2h,共收割小麦3.6hm2;4台大收割机和3台小收割机均工作5h,共收割小麦11hm2.问1台大收割机和1台小收割机每小时各收割小麦多少公顷?
如图,2台大收割机和5台小收割机均工作2h,共收割小麦3.6hm2;4台大收割机和3台小收割机均工作5h,共收割小麦11hm2.问1台大收割机和1台小收割机每小时各收割小麦多少公顷? 如图,小明家五月份医疗支出费用为140元,则其他支出占
如图,小明家五月份医疗支出费用为140元,则其他支出占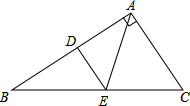 如图,在直角△ABC中,∠BAC=90°,AB=8,AC=6,DE是AB边的垂直平分线,垂足为D,交边BC于点E,连接AE,则△ACE的周长为
如图,在直角△ABC中,∠BAC=90°,AB=8,AC=6,DE是AB边的垂直平分线,垂足为D,交边BC于点E,连接AE,则△ACE的周长为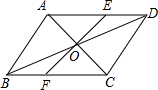 如图所示,过平行四边形ABCD对角线的交点0,分别交AD于点E,交BC于点F,若0E=5,四边形CDEF的周长为25,则平行四边形ABCD的周长为
如图所示,过平行四边形ABCD对角线的交点0,分别交AD于点E,交BC于点F,若0E=5,四边形CDEF的周长为25,则平行四边形ABCD的周长为