题目内容
12.公元前5世纪,毕达哥拉斯学派中的一名成员希伯索斯发现了无理数$\sqrt{2}$,导致了第一次数学危机,$\sqrt{2}$是无理数的证明如下:假设$\sqrt{2}$是有理数,那么它可以表示成$\frac{q}{p}$(p与q是互质的两个正整数).于是($\frac{q}{p}$)2=($\sqrt{2}$)2=2,所以,q2=2p2.于是q2是偶数,进而q是偶数,从而可设q=2m,所以(2m)2=2p2,p2=2m2,于是可得p也是偶数.这与“p与q是互质的两个正整数”矛盾.从而可知“$\sqrt{2}$是有理数”的假设不成立,所以,$\sqrt{2}$是无理数.
这种证明“$\sqrt{2}$是无理数”的方法是( )
| A. | 综合法 | B. | 反证法 | C. | 举反例法 | D. | 数学归纳法 |
分析 利用反证法的一般步骤是:①假设命题的结论不成立;②从这个假设出发,经过推理论证,得出矛盾;③由矛盾判定假设不正确,从而肯定原命题的结论正确,进而判断即可.
解答 解:由题意可得:这种证明“$\sqrt{2}$是无理数”的方法是反证法.
故选:B.
点评 此题主要考查了反证法,正确把握反证法的一般步骤是解题关键.

练习册系列答案
相关题目
2. 如图所示的几何体的主视图是( )
如图所示的几何体的主视图是( )
 如图所示的几何体的主视图是( )
如图所示的几何体的主视图是( )| A. |  | B. |  | C. |  | D. |  |
3.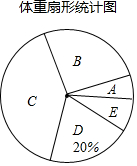 某校为了解九年级学生的体重情况,随机抽取了九年级部分学生进行调查,将抽取学生的体重情况绘制如下不完整的统计图表,如图表所示,请根据图表信息回答下列问题:
某校为了解九年级学生的体重情况,随机抽取了九年级部分学生进行调查,将抽取学生的体重情况绘制如下不完整的统计图表,如图表所示,请根据图表信息回答下列问题:
体重频数分布表
(1)填空:①m=52(直接写出结果);
②在扇形统计图中,C组所在扇形的圆心角的度数等于144度;
(2)如果该校九年级有1000名学生,请估算九年级体重低于60千克的学生大约有多少人?
 某校为了解九年级学生的体重情况,随机抽取了九年级部分学生进行调查,将抽取学生的体重情况绘制如下不完整的统计图表,如图表所示,请根据图表信息回答下列问题:
某校为了解九年级学生的体重情况,随机抽取了九年级部分学生进行调查,将抽取学生的体重情况绘制如下不完整的统计图表,如图表所示,请根据图表信息回答下列问题:体重频数分布表
| 组边 | 体重(千克) | 人数 |
| A | 45≤x<50 | 12 |
| B | 50≤x<55 | m |
| C | 55≤x<60 | 80 |
| D | 60≤x<65 | 40 |
| E | 65≤x<70 | 16 |
②在扇形统计图中,C组所在扇形的圆心角的度数等于144度;
(2)如果该校九年级有1000名学生,请估算九年级体重低于60千克的学生大约有多少人?
20.下列运算正确的是( )
| A. | a3+a3=a6 | B. | (a-b)2=a2-b2 | C. | (-a3)2=a6 | D. | a12÷a2=a6 |
7.下列运算结果为正数的是( )
| A. | (-3)2 | B. | -3÷2 | C. | 0×(-2017) | D. | 2-3 |
17.下列运算正确的是( )
| A. | 5x-3x=2 | B. | (x-1)2=x2-1 | C. | (-2x2)3=-6x6 | D. | x6÷x2=x4 |
4.下列运算正确的是( )
| A. | 3a-a=2 | B. | (a2)3=a5 | C. | a2•a3=a5 | D. | a6÷a3=a2 |
1.某市今年约有140000人报名参加初中学业水平考试,用科学记数法表示140000为( )
| A. | 14×104 | B. | 14×103 | C. | 1.4×104 | D. | 1.4×105 |