题目内容
先写出下列问题中的函数关系式,然后指出其中的变量和常量.
(1)用20cm的铁丝所围的长方形的长xcm与面积Scm2的关系;
(2)直角三角形中一个锐角α与另一个锐角β之间的关系;
(3)等腰三角形的顶角为x度,试用x表示底角y的度数;
(4)一个铜球在0℃的体积为1 000cm3,加热后温度每增加1℃,体积增加0.051cm3,t℃时球的体积为Vcm3.
(1)用20cm的铁丝所围的长方形的长xcm与面积Scm2的关系;
(2)直角三角形中一个锐角α与另一个锐角β之间的关系;
(3)等腰三角形的顶角为x度,试用x表示底角y的度数;
(4)一个铜球在0℃的体积为1 000cm3,加热后温度每增加1℃,体积增加0.051cm3,t℃时球的体积为Vcm3.
考点:函数关系式,常量与变量
专题:计算题
分析:(1)由长方形的面积公式S=长×宽来写函数关系式;
(2)由“直角三角形的两个锐角互余”来写函数关系式;
(3)由“等腰三角形的性质和三角形内角和是180°”来写函数关系式;
(4)t℃时球的体积=0℃的体积+增加的体积.
(2)由“直角三角形的两个锐角互余”来写函数关系式;
(3)由“等腰三角形的性质和三角形内角和是180°”来写函数关系式;
(4)t℃时球的体积=0℃的体积+增加的体积.
解答:解:(1)S=(20÷2-x)x=-x2+10x(0<x<10),即S=-x2+10x(0<x<10);
其中10是常量,x与S是变量;
(2)α=90°-β.90°是常量,α、β是变量
(3)y=
=90-
,即y=90-
(0<x<180°).其中,90,
是常量,x、y是变量;
(4)V=1000+0.051t.其中1000的常量,tV是变量.
其中10是常量,x与S是变量;
(2)α=90°-β.90°是常量,α、β是变量
(3)y=
| 180-x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| 1 |
| 2 |
(4)V=1000+0.051t.其中1000的常量,tV是变量.
点评:本题考查了函数关系式:根据实际问题的数量关系用解析式法表示实际问题中两变化的量之间的关系.

练习册系列答案
相关题目
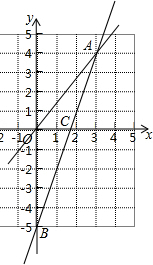 如图,一个正比例函数y1=k1x的图象与一个一次函数y2=k2x+b的图象相交于点A(3,4),且一次函数y2的图象与y轴相交于点B(0,-5),与x轴交于点C.
如图,一个正比例函数y1=k1x的图象与一个一次函数y2=k2x+b的图象相交于点A(3,4),且一次函数y2的图象与y轴相交于点B(0,-5),与x轴交于点C. 如图,在△ABC中,以AB为直径的⊙O交AC于点M,弦MN∥BC交AB 于点E,且ME=3,AM=6,AE=3
如图,在△ABC中,以AB为直径的⊙O交AC于点M,弦MN∥BC交AB 于点E,且ME=3,AM=6,AE=3
