题目内容
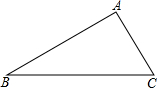 如图,在Rt△ABC中,∠A=90°,∠B=30°,BC=10,以A为圆心画圆,如果⊙A与直线BC相切,那么⊙A的半径长为
如图,在Rt△ABC中,∠A=90°,∠B=30°,BC=10,以A为圆心画圆,如果⊙A与直线BC相切,那么⊙A的半径长为考点:切线的性质
专题:
分析:此题可以转化为求斜边BC上的高的问题;在Rt△ABC中,∠B=30°,可知∠C=60°;进而在Rt△ADC中,由AC及∠C的正弦值可求得AD的长,即⊙A的半径.
解答:解:过点A作AD⊥BC,
∵∠A=90°,∠B=30°,
∴∠C=60°
∵BC=10,
∴AC=
BC=5,
∴AD=AC•sin60°=
,
故答案为:
.

∵∠A=90°,∠B=30°,
∴∠C=60°
∵BC=10,
∴AC=
| 1 |
| 2 |
∴AD=AC•sin60°=
| 5 |
| 2 |
| 3 |
故答案为:
| 5 |
| 2 |
| 3 |
点评:此题考查了切线的性质,将由切线求半径的问题转化为解直角三角形的问题是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,该图是由4个相同的小正方体组成的几何体,其俯视图为( )
如图,该图是由4个相同的小正方体组成的几何体,其俯视图为( )A、 |
B、 |
C、 |
D、 |
 某海防哨所O发现在他的东偏北60°方向,距离哨所400m的A处有一艘船向正东方向航行,经过2分钟后到达哨所的东北方向的B处,问船从A处到B处航速是多少千米/小时(精确到1千米/小时)?(参考数据
某海防哨所O发现在他的东偏北60°方向,距离哨所400m的A处有一艘船向正东方向航行,经过2分钟后到达哨所的东北方向的B处,问船从A处到B处航速是多少千米/小时(精确到1千米/小时)?(参考数据
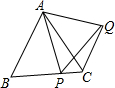 如图,△ABC为等边三角形,P为BC上一点,△APQ为等边三角形.有下列结论:
如图,△ABC为等边三角形,P为BC上一点,△APQ为等边三角形.有下列结论: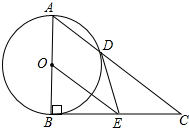 如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连接DE、OE.
如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连接DE、OE.