题目内容
 某海防哨所O发现在他的东偏北60°方向,距离哨所400m的A处有一艘船向正东方向航行,经过2分钟后到达哨所的东北方向的B处,问船从A处到B处航速是多少千米/小时(精确到1千米/小时)?(参考数据
某海防哨所O发现在他的东偏北60°方向,距离哨所400m的A处有一艘船向正东方向航行,经过2分钟后到达哨所的东北方向的B处,问船从A处到B处航速是多少千米/小时(精确到1千米/小时)?(参考数据| 2 |
| 3 |
| 5 |
考点:解直角三角形的应用-方向角问题
专题:
分析:根据题意先画出图形,再分别解直角三角形AOC与直角三角形BOC,求出AC=200米,BC=200
米,然后根据AB=BC-AC求出AB的长,则问题可求.
| 3 |
解答: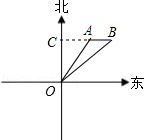 解:作AC⊥OC于点C.
解:作AC⊥OC于点C.
由题意有OA=400米,
在直角三角形AOC中,∠AOC=90°-60°=30°,
所以AC=200米,OC=200
米.
在直角三角形OBC中,∠BOC=45°,
所以,BC=OC=200
米,
所以AB=BC-AC=200
-200米,
所以速度为(200
-200)÷2=100
-100(米/分)≈4千米/时.
答:船从A处到B处航速约是4千米/小时.
 解:作AC⊥OC于点C.
解:作AC⊥OC于点C.由题意有OA=400米,
在直角三角形AOC中,∠AOC=90°-60°=30°,
所以AC=200米,OC=200
| 3 |
在直角三角形OBC中,∠BOC=45°,
所以,BC=OC=200
| 3 |
所以AB=BC-AC=200
| 3 |
所以速度为(200
| 3 |
| 3 |
答:船从A处到B处航速约是4千米/小时.
点评:本题考查了解直角三角形的应用-方向角问题,涉及到锐角三角函数、实数的运算、解直角三角形,难度适中.体现了数学与生活的密切联系,同时也进行了实数运算方面的进一步考查,根据题意准确画出图形是解题的关键.

练习册系列答案
相关题目
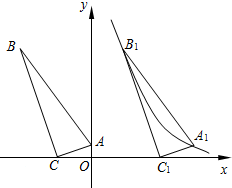 如图,在平面直角坐标系中有Rt△ABC,∠ACB=90°,A(0,1),
如图,在平面直角坐标系中有Rt△ABC,∠ACB=90°,A(0,1),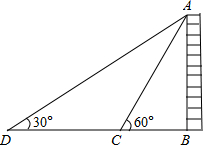 如图,为测量某物体AB的高度,在D点测得A点的仰角为30°,朝物体AB方向前进20米,到达点C,再次测得点A的仰角为60°,则物体AB的高度为多少?
如图,为测量某物体AB的高度,在D点测得A点的仰角为30°,朝物体AB方向前进20米,到达点C,再次测得点A的仰角为60°,则物体AB的高度为多少?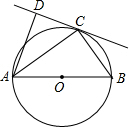 已知:AB为⊙O的直径,C为⊙O上一点,CD是⊙O的切线,AD⊥CD于D.
已知:AB为⊙O的直径,C为⊙O上一点,CD是⊙O的切线,AD⊥CD于D. 如图,AB是⊙O的切线,切点为A,OA=1,∠AOB=60°,则图中阴影部分的面积是
如图,AB是⊙O的切线,切点为A,OA=1,∠AOB=60°,则图中阴影部分的面积是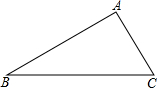 如图,在Rt△ABC中,∠A=90°,∠B=30°,BC=10,以A为圆心画圆,如果⊙A与直线BC相切,那么⊙A的半径长为
如图,在Rt△ABC中,∠A=90°,∠B=30°,BC=10,以A为圆心画圆,如果⊙A与直线BC相切,那么⊙A的半径长为