题目内容
已知x为整数,且
-
+
为正整数,则整数x= .
| 2 |
| x+3 |
| 2 |
| x-3 |
| 2x+18 |
| x2-9 |
考点:分式的化简求值
专题:计算题
分析:先通分,再进行同分母分式的加减运算得到原式=
,约分得到原式=
,由于x为整数,且
为正整数,根据整数的整除性得到x-3=1或x-3=2,然后解一次方程即可.
| 2(x+3) |
| (x+3)(x-3) |
| 2 |
| x-3 |
| 2 |
| x-3 |
解答:解:
-
+
=
-
+
=
=
,
∵x为整数,
-
+
为正整数,
∴x为整数,且
为正整数,
∴x-3=1或x-3=2,
∴x=4或x=5.
故答案为4或5.
| 2 |
| x+3 |
| 2 |
| x-3 |
| 2x+18 |
| x2-9 |
| 2(x-3) |
| (x+3)(x-3) |
| 2(x+3) |
| (x+3)(x-3) |
| 2x+18 |
| (x+3)(x-3) |
=
| 2(x+3) |
| (x+3)(x-3) |
=
| 2 |
| x-3 |
∵x为整数,
| 2 |
| x+3 |
| 2 |
| x-3 |
| 2x+18 |
| x2-9 |
∴x为整数,且
| 2 |
| x-3 |
∴x-3=1或x-3=2,
∴x=4或x=5.
故答案为4或5.
点评:本题考查了分式的化简求值:先把分式的分子或分母因式分解(有括号,先算括号),然后约分得到最简分式或整式,然后把满足条件的字母的值代入计算得到对应的分式的值.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
下列运算正确的是( )
| A、a3-a2=a |
| B、a8÷a2=a4 |
| C、(3a)3=9a3 |
| D、(a3)2=a6 |
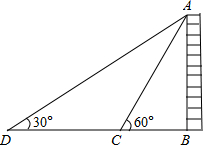 如图,为测量某物体AB的高度,在D点测得A点的仰角为30°,朝物体AB方向前进20米,到达点C,再次测得点A的仰角为60°,则物体AB的高度为多少?
如图,为测量某物体AB的高度,在D点测得A点的仰角为30°,朝物体AB方向前进20米,到达点C,再次测得点A的仰角为60°,则物体AB的高度为多少? 若一次函数y=kx+b(k,b为常数,且k=0)的图象如图,根据图象信息,则关于x的不等式kx+b>3的解为
若一次函数y=kx+b(k,b为常数,且k=0)的图象如图,根据图象信息,则关于x的不等式kx+b>3的解为 如图,在Rt△ABC中,∠A=90°,∠B=30°,BC=10,以A为圆心画圆,如果⊙A与直线BC相切,那么⊙A的半径长为
如图,在Rt△ABC中,∠A=90°,∠B=30°,BC=10,以A为圆心画圆,如果⊙A与直线BC相切,那么⊙A的半径长为