题目内容
如图，⊙O中，AD、BC是圆O的弦，OA⊥BC，∠AOB=50°，CE⊥AD，则∠DCE的度数是（ ）
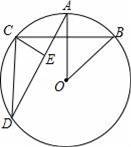
A．25° B．65° C．45° D．55°
B【考点】圆周角定理；垂径定理．
【分析】由OA⊥BC，根据垂径定理的即可求得
=
，又由圆周角定理可求得∠D=
∠AOB=×50°=25°，再由CE⊥AD，即可求得∠DCE的度数．
【解答】解：∵OA⊥BC，
∴=，
∴∠D=∠AOB=×50°=25°，
∵CE⊥AD，
∴∠DCE=90°﹣∠D=65°．
故选B．
【点评】此题考查了圆周角定理以及垂径定理．注意在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
中自变量x的取值范围为（ ）
