题目内容
17.已知x2-3x+1=0,求下列代数式的值:(1)x2+x-2;
(2)(x-$\frac{1}{x}$)2;
(3)x4-2x3-5x+2.
分析 (1)把x2-3x+1=0两边都除以x得:x-3+$\frac{1}{x}$=0,即x+$\frac{1}{x}$=3,代入x2+x-2=(x+$\frac{1}{x}$)2-2可得;
(2)将(1)中结果代入(x-$\frac{1}{x}$)2=x2+$\frac{1}{{x}^{2}}$-2可得;
(3)由原式得x4=3x3-x2,x3=3x2-x,代入后逐步化简可得.
解答 解:(1)∵x2-3x+1=0,且x≠0,
∴两边都除以x得:x-3+$\frac{1}{x}$=0,即x+$\frac{1}{x}$=3,
则x2+x-2=(x+$\frac{1}{x}$)2-2=9-2=7;
(2)(x-$\frac{1}{x}$)2=x2+$\frac{1}{{x}^{2}}$-2=7-2=5;
(3)∵x2-3x+1=0,
∴x2=3x-1,
∴x4=3x3-x2,x3=3x2-x,
则原式=3x3-x2-2x3-5x+2
=x3-x2-5x+2
=3x2-x-x2-5x+2
=2x2-6x+2
=2(x2-3x+1)
=0.
点评 本题主要考查因式分解的应用,熟练掌握等式的基本性质及整体代入思想的运用是解题的关键.

练习册系列答案
相关题目
12.为鼓励居民节约用电,某市试行每户每月阶段电价加收费制,具体执行方案如表:
例如:一户居民七月份用电400度,则需缴电费200×0.55+100×0.65+100×0.85=260(元).
(1)若小莹家六月份用电360度,则需缴电费多少元?
(2)已知小悦家五、六月份共用电540度,其中六月份用电量大于五月份用电量,共缴电费317元,问小悦家五、六月份各用电多少度?
| 每户每月用电数(度)阶段 | 阶段电价(元/度) |
| 小于等于200 | 0.55 |
| 大于200小于300的部分 | 0.65 |
| 大于等于300小于400的部分 | 0.8 |
| 大于等于400的部分 | 1 |
(1)若小莹家六月份用电360度,则需缴电费多少元?
(2)已知小悦家五、六月份共用电540度,其中六月份用电量大于五月份用电量,共缴电费317元,问小悦家五、六月份各用电多少度?
2.下列关于等边三角形的描述错误的是( )
| A. | 三边相等的三角形是等边三角形 | |
| B. | 三个角相等的三角形是等边三角形 | |
| C. | 有一个角是60°的三角形是等边三角形 | |
| D. | 有两个角是60°的三角形是等边三角形 |
9.按下面的程序计算:

当输入x=100时,输出结果是299;当输入x=50时,输出结果是466;如果输入x的值是正整数,输出结果是257,那么满足条件的x的值最多有( )

当输入x=100时,输出结果是299;当输入x=50时,输出结果是466;如果输入x的值是正整数,输出结果是257,那么满足条件的x的值最多有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.下列判断中错误的是( )
| A. | 有两角和一边对应相等的两个三角形全等 | |
| B. | 有两边和一角对应相等的两个三角形全等 | |
| C. | 有两边和其中一边上的中线对应相等的两个三角形全等 | |
| D. | 有一边对应相等的两个等边三角形全等 |

 cm
cm cm
cm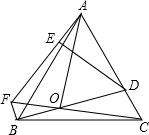 如图,点O为等边△ABC内一点,OA=2$\sqrt{5}$,OC=$\sqrt{15}$,连接BO并延长交AC于点D,且∠DOC=30°,过点B作BF⊥BD交CO延长线于点F,连接AF,过点D作DE⊥AF于点E,则DE=$\frac{5\sqrt{5}}{3}$.
如图,点O为等边△ABC内一点,OA=2$\sqrt{5}$,OC=$\sqrt{15}$,连接BO并延长交AC于点D,且∠DOC=30°,过点B作BF⊥BD交CO延长线于点F,连接AF,过点D作DE⊥AF于点E,则DE=$\frac{5\sqrt{5}}{3}$. 在四边形ABCD中,已知AB=AD=8,∠A=60°,∠D=150°,四边形的周长为32.
在四边形ABCD中,已知AB=AD=8,∠A=60°,∠D=150°,四边形的周长为32.