题目内容
20.某个体户购进一批时令水果,20天销售完毕,他将本次销售情况进行了跟踪记录,根据所记录的数据绘制如下的函数图象,其中日销售量y(千克)与销售时间x(天)之间的函数关系如图(1)所示,销售单价p(元/千克)与销售时间x(天)之间的函数关系如图(2)所示.(销售额=销售单价×销售量).
(1)从图(1)可知.第6天日销售量为12千克,第18天日销售为12千克.
(2)求第6天和第18天的销售额;
(3)若日销售量不低于24千克的时间段为“最佳销售期”,则此次销售过程中,“最佳销售期”共有多少天?在此期间销售单价最高为多少元?
分析 (1)待定系数法分别求出0≤x≤15、15<x≤20时销售量y关于销售时间x的函数关系式,再分别求当x=6和x=18时y的值即可;
(2)由图(2)先求出0≤x<10、10≤x≤20时销售单价p关于销售时间x的函数关系式,求出x=6和x=18时的销售单价,最后根据销售额=销售单价×销售量分别求之;
(3)分别求出0≤x≤15、15<x≤20时销售量y≥24时x的范围,可知共有多少天,结合上述x的范围根据一次函数性质求p的最大值即可.
解答 解:(1)当0≤x≤15时,y=kx,
将(15,30)代入得,30=15k,
解得:k=2,即y=2x,
当x=6时,y=2×6=12;
故第6天日销售量为12千克;
当15<x≤20时,设y=k1x+b,
将(15,30)、(20,0)代入得:$\left\{\begin{array}{l}{15{k}_{1}+b=30}\\{20{k}_{1}+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=-6}\\{b=120}\end{array}\right.$,
即y=-6x+120,
当x=18时,y=-6×18+120=12;
故第18天日销售量为12千克;
(2)∵第6天日销售量为12千克,销售单价为10元/千克,
∴第6天日销售额为12×10=120(元);
当10≤x≤20时,设销售单价p与销售时间x之间的函数关系式为p=mx+n,
∵点(10,10)、(20,8)在p=mx+n的图象上,
∴$\left\{\begin{array}{l}{10m+n=10}\\{20m+n=8}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=-\frac{1}{5}}\\{n=12}\end{array}\right.$,
∴p=-$\frac{1}{5}$x+12(10≤x≤20),
当x=18时,p=-$\frac{1}{5}$×18+12=8.4,y=12,
故销售额为:8.4×12=100.8(元),
综上,第6天和第18天的销售金额分别为120元、100.8元;
(3)根据题意,若日销售量不低于24千克,则y≥24,
当0≤x≤15时,y=2x,解不等式2x≥24,得x≥12;
当15<x≤20时,y=-6x+120,解不等式-6x+120≥24,得x≤16;
∴12≤x≤16,
故最佳销售期共有5天;
∵p=-$\frac{1}{5}$x+12(10≤x≤20)中,-$\frac{1}{5}$<0,
∴p随x的增大而减小,
∴当12≤x≤16时,当x=12时,p取得最大值,最大值为-$\frac{1}{5}$×12+12=9.6,
故此次销售过程中最佳销售期共有5天,在此期间销售单价最高为9.6元/千克.
故答案为:(1)12,12.
点评 本题主要考查一次函数的实际应用能力,根据题意分类求解是解题的关键.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案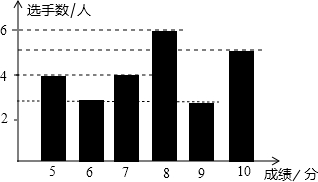 某校举行学生“爱校•爱家•爱国”主题演讲比赛,某同学将选手们的得分进行统计,绘制成如图所示的得分条形图下列四个判断:
某校举行学生“爱校•爱家•爱国”主题演讲比赛,某同学将选手们的得分进行统计,绘制成如图所示的得分条形图下列四个判断:①共有10人得6分;
②得5分和7分的人数一样多;
③8名选手的成绩高于8分;
④共有25名选手参赛.
其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | (5,8) | B. | (5,-2) | C. | (-11,-2) | D. | (-11,8) |
| A. | m-2>n-2 | B. | $\frac{m}{2}>\frac{n}{2}$ | C. | -2m>-2n | D. | m+2>n+2 |
| A. | 637×108元 | B. | 63.7×109元 | C. | 6.4×1010元 | D. | 6.37×1010元 |
| A. | $\frac{1}{2015}$ | B. | -2015 | C. | 2015 | D. | -$\frac{1}{2015}$ |
 如图,面积为20的正方形的一边AB落在数轴上,且点A与原点O重合,则该数轴上一个刻度表示2个单位长度.
如图,面积为20的正方形的一边AB落在数轴上,且点A与原点O重合,则该数轴上一个刻度表示2个单位长度.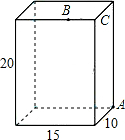 如图,一个无盖的长方体盒子的长为15cm,宽为10cm,高为20cm,点B离点C的距离为
如图,一个无盖的长方体盒子的长为15cm,宽为10cm,高为20cm,点B离点C的距离为