题目内容
6. 已知,如图:AD、BC相交于点O,AD=BC,∠C=∠D=90°.求证:AO=BO,CO=DO.
已知,如图:AD、BC相交于点O,AD=BC,∠C=∠D=90°.求证:AO=BO,CO=DO.
分析 利用HL证明Rt△ACB≌Rt△ADB,得到∠ABC=∠BAD,所以OA=OB,又由AD=BC,所以AD-OA=BC-OB,即OD=OC.
解答 解:∵∠C=∠D=90°,
∴△ACB和△ADB为直角三角形,
在Rt△ACB和Rt△ADB中,
$\left\{\begin{array}{l}{AD=BC}\\{AB=BA}\end{array}\right.$
∴Rt△ACB≌Rt△ADB,
∴∠ABC=∠BAD,
∴OA=OB,
∵AD=BC,
∴AD-OA=BC-OB,
即OD=OC.
点评 本题考查了全等三角形的性质与判定,解决本题的关键是证明Rt△ACB≌Rt△ADB.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
17.下列式子中是最简二次根式的是( )
| A. | $\sqrt{\frac{1}{3}}$ | B. | $\sqrt{27}$ | C. | $\sqrt{0.25}$ | D. | $\sqrt{30}$ |
14. 如图,△ABC≌△DCB,如果AB=7cm,BC=12cm,AC=9cm,那BD的长是( )
如图,△ABC≌△DCB,如果AB=7cm,BC=12cm,AC=9cm,那BD的长是( )
 如图,△ABC≌△DCB,如果AB=7cm,BC=12cm,AC=9cm,那BD的长是( )
如图,△ABC≌△DCB,如果AB=7cm,BC=12cm,AC=9cm,那BD的长是( )| A. | 7cm | B. | 9cm | C. | 12cm | D. | 无法确定 |
11.下列说法中,正确的是( )
| A. | 有理数中没有最大的负整数 | B. | 有理数中没有最大的正整数 | ||
| C. | 同号两数相加的和一定比加数大 | D. | 异号两数相加的和一定比加数小 |
16.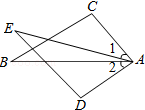 如图,已知∠1=∠2,AC=AD,增加下列条件:其中不能使△ABC≌△AED的条件( )
如图,已知∠1=∠2,AC=AD,增加下列条件:其中不能使△ABC≌△AED的条件( )
 如图,已知∠1=∠2,AC=AD,增加下列条件:其中不能使△ABC≌△AED的条件( )
如图,已知∠1=∠2,AC=AD,增加下列条件:其中不能使△ABC≌△AED的条件( )| A. | AB=AE | B. | BC=ED | C. | ∠C=∠D | D. | ∠B=∠E |
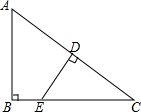 如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,点D是AC中点,过点D作DE⊥AC交BC于点E,则CE的长度是$\frac{25}{4}$.
如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,点D是AC中点,过点D作DE⊥AC交BC于点E,则CE的长度是$\frac{25}{4}$. 如图,在菱形ABCD中,对角线AC、BD相交于点O,AC=6,BD=8,点P是AC延长线上的一个动点,过点P作PE⊥AD,垂足为E,作CD延长线的垂线,垂足为E,则|PE-PF|=4.8.
如图,在菱形ABCD中,对角线AC、BD相交于点O,AC=6,BD=8,点P是AC延长线上的一个动点,过点P作PE⊥AD,垂足为E,作CD延长线的垂线,垂足为E,则|PE-PF|=4.8.