题目内容
2.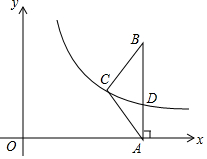 如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=$\frac{k}{x}$(x>0)的图象经过点C,交AB于点D.已知AB=4,BC=$\frac{5}{2}$.
如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=$\frac{k}{x}$(x>0)的图象经过点C,交AB于点D.已知AB=4,BC=$\frac{5}{2}$.(1)若OA=4,求k的值;
(2)连接OC,若BD=BC,求OC的长.
分析 (1)利用等腰三角形的性质得出AE,BE的长,再利用勾股定理得出OA的长,得出C点坐标即可得出答案;
(2)首先表示出D,C点坐标进而利用反比例函数图象上的性质求出C点坐标,再利用勾股定理得出CO的长.
解答 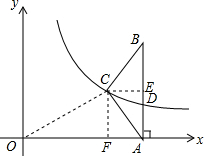 解:(1)作CE⊥AB,垂足为E,
解:(1)作CE⊥AB,垂足为E,
∵AC=BC,AB=4,
∴AE=BE=2.
在Rt△BCE中,BC=$\frac{5}{2}$,BE=2,
∴CE=$\frac{3}{2}$,
∴CE=$\frac{3}{2}$,
∵OA=4,
∴C点的坐标为:($\frac{5}{2}$,2),
∵点C在$y=\frac{k}{x}$的图象上,
∴k=5,
(2)设A点的坐标为(m,0),
∵BD=BC=$\frac{5}{2}$,
∴AD=$\frac{3}{2}$,
∴D,C两点的坐标分别为:(m,$\frac{3}{2}$),(m-$\frac{3}{2}$,2).
∵点C,D都在$y=\frac{k}{x}$的图象上,
∴$\frac{3}{2}$m=2(m-$\frac{3}{2}$),
∴m=6,
∴C点的坐标为:($\frac{9}{2}$,2),
作CF⊥x轴,垂足为F,
∴OF=$\frac{9}{2}$,CF=2,
在Rt△OFC中,
OC2=OF2+CF2,
∴OC=$\frac{\sqrt{97}}{2}$.
点评 此题主要考查了等腰三角形的性质以及勾股定理和反比例函数图象上的性质,正确得出C点坐标是解题关键.

练习册系列答案
相关题目
12.我们知道方程x2+2x-3=0的解是x1=1,x2=-3,现给出另一个方程(2x+3)2+2(2x+3)-3=0,它的解是( )
| A. | x1=1,x2=3 | B. | x1=1,x2=-3 | C. | x1=-1,x2=3 | D. | x1=-1,x2=-3 |