题目内容
16. 如图,在⊙O中,AB为⊙O的直径,AB=4.动点P从A点出发,以每秒π个单位的速度在⊙O上按顺时针方向运动一周.设动点P的运动时间为t秒,点C是圆周上一点,且∠AOC=40°,当t=$\frac{4}{9}$或$\frac{14}{9}$或$\frac{22}{9}$或$\frac{32}{9}$秒时,点P与点C中心对称,且对称中心在直径AB上.
如图,在⊙O中,AB为⊙O的直径,AB=4.动点P从A点出发,以每秒π个单位的速度在⊙O上按顺时针方向运动一周.设动点P的运动时间为t秒,点C是圆周上一点,且∠AOC=40°,当t=$\frac{4}{9}$或$\frac{14}{9}$或$\frac{22}{9}$或$\frac{32}{9}$秒时,点P与点C中心对称,且对称中心在直径AB上.
分析 根据中心对称的定义,可得P点的位置,根据弧长公式,可得$\widehat{AP}$,根据路程除以速度等于时间,可得答案.
解答 解:如图 ,
,
当∠AOP1=40°时,P1与C1对称,$\widehat{A{P}_{1}}$=4π×$\frac{40}{360}$=$\frac{4π}{9}$,t=$\frac{4π}{9}$÷π=$\frac{4}{9}$;
当∠AOP2=140°时,P2与C1对称,$\widehat{A{P}_{2}}$=4π×$\frac{140}{360}$=$\frac{14}{9}$π,t=$\frac{14π}{9}$÷π=$\frac{14}{9}$;
当∠AOP3=220°时,P3与C2对称,$\widehat{A{P}_{3}}$=4π×$\frac{220}{360}$=$\frac{22π}{9}$,t=$\frac{22π}{9}$÷π=$\frac{22}{9}$;
当∠AOP4=320°时,P4与C1对称,$\widehat{A{P}_{4}}$=4π×$\frac{320}{360}$=$\frac{32}{9}$π,t=$\frac{32π}{9}$÷π=$\frac{32}{9}$;
故答案为:$\frac{4}{9}$或$\frac{14}{9}$或$\frac{22}{9}$或$\frac{32}{9}$.
点评 本题考查了中心对称,利用中心对称得出P点的位置是解题关键,又利用了弧长公式,要分类讨论,以防遗漏.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.已知△ABC中,AB=AC,∠B=50°,则∠C的度数为( )
| A. | 50° | B. | 65° | C. | 80° | D. | 50°或65° |
1.函数y=-x2-3的图象向上平移2个单位,再向左平移2个单位后,得到的函数是( )
| A. | y=-(x+2)2-1 | B. | y=-(x-2)2-1 | C. | y=-(x-2)2+1 | D. | y=-(x+2)2+1 |
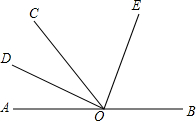 如图,O为直线AB上一点,∠AOC=52°,OD平分∠AOC,∠DOE=90°.
如图,O为直线AB上一点,∠AOC=52°,OD平分∠AOC,∠DOE=90°.