题目内容
17.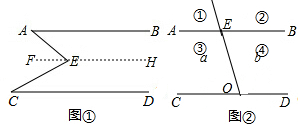 (1)如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,EC.探究∠AEC,∠EAB,∠ECD之间的关系.
(1)如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,EC.探究∠AEC,∠EAB,∠ECD之间的关系.阅读下面的说理过程,并填写适当的理由或数学式:
过点E画FH∥AB
∴∠EAB=∠AEF (两直线平行,内错角相等)
∵AB∥CD(已知),
FH∥AB(作图).
∴FH∥CD (如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
∴∠ECD=∠CEF (两直线平行,内错角相等)
∠AEC=∠AEF+∠CEF
∴∠AEC=∠EAB+∠ECD (等式的性质)
(2)如图2,AB∥CD,射线OE与CD 交于点O,与AB交于点E,①②③④分别是被射线OE隔开的4个区域(不含边界),P是位于以上四个区域上的点,猜想:∠PEB,∠POD,∠EPO之间的关系(不要求说理).
分析 (1)过点E画FH∥AB,根据平行线的性质,即可得到∠EAB=∠AEF,∠ECD=∠CEF,根据∠AEC=∠AEF+∠CEF,即可得到∠AEC=∠EAB+∠ECD;
(2)根据点P在①②③④4个区域,分别画出图形,依据平行线的性质以及三角形外角性质,即可得到PEB,∠POD,∠EPO之间的关系.
解答 解:(1)过点E画FH∥AB,∴∠EAB=∠AEF(两直线平行,内错角相等),
∵AB∥CD(已知),
FH∥AB(作图).
∴FH∥CD(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
∴∠ECD=∠CEF(两直线平行,内错角相等),
∵∠AEC=∠AEF+∠CEF,
∴∠AEC=∠EAB+∠ECD(等式的性质),
故答案为:两直线平行,内错角相等; 如果两条直线都与第三条直线平行,那么这两条直线也互相平行;两直线平行,内错角相等;∠EAB,∠ECD;
(2)如图,点P在区域①时,∠EPO=∠PEB-∠POD;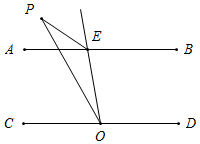
如图,点P在区域②时,∠EPO=∠POD-∠PEB; 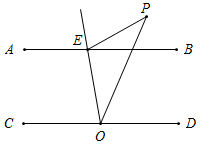
如图,点P在区域③时,∠EPO=360°-(∠PEB+∠POD); 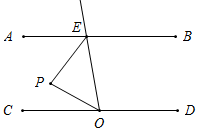
如图,点P在区域④时,∠EPO=∠PEB+∠POD.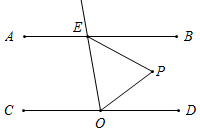
点评 本题主要考查了平行线的性质与判定,解决问题的关键是作辅助线构造内错角,解题时注意:平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.

练习册系列答案
相关题目
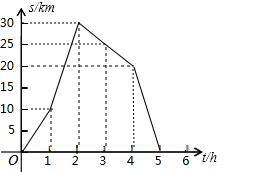 如图是小李骑自行车离家的距离s(km)与时间t(h)之间的关系.
如图是小李骑自行车离家的距离s(km)与时间t(h)之间的关系.