题目内容
9.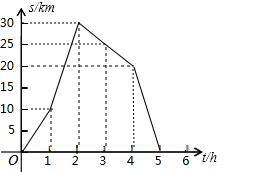 如图是小李骑自行车离家的距离s(km)与时间t(h)之间的关系.
如图是小李骑自行车离家的距离s(km)与时间t(h)之间的关系.(1)在这个变化过程中自变量是离家时间,因变量是离家距离;
(2)小李何时到达离家最远的地方?此时离家多远?
(3)请直接写出小李何时与家相距20km?
(4)求出小李这次出行的平均速度.
分析 (1)在坐标系中横坐标是自变量,纵坐标是因变量,据此求解;
(2)根据图象可以得到离家最远时的时间,此时离家的距离,据此即可确定;
(3)根据图象可以得到有两个时间点,据此即可确定;
(4)往返所用的总路程除以总时间可得.
解答 解:(1)在这个变化过程中自变量是离家时间,因变量是离家距离,
故答案为:离家时间、离家距离;
(2)根据图象可知小李2h后到达离家最远的地方,此时离家30km;
(3)当1≤t≤2时,设s=kt+b,
将(1,10)、(2,30)代入,得:$\left\{\begin{array}{l}{k+b=10}\\{2k+b=30}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=20}\\{b=-10}\end{array}\right.$,
∴s=20t-10,
当s=20时,有20t-10=20,
解得t=1.5,
由图象知,当t=4时,s=20,
故当t=1.5或t=4时,小李与家相距20km;
(4)小李这次出行的平均速度为$\frac{30+30}{5}$=12(km/h).
点评 本题考查了一次函数的图象,根据图象正确理解s随t的增大的变化情况是关键.

练习册系列答案
相关题目
18.用每分可抽30t水的抽水机来抽污水管道内的污水,估计积存的污水超过1200t而不足1500t,则将污水抽完所用时间x的取值范围是( )
| A. | 40<x≤50 | B. | 40≤x<50 | C. | 40<x<50 | D. | 40≤x≤50 |
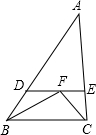 如图,在△ABC中,已知∠ABC和∠ACB的平分线交于点F,过F作DE∥BC,交AB于点D,交AC于点E,若BD+CE=10,则线段DE的长为10.
如图,在△ABC中,已知∠ABC和∠ACB的平分线交于点F,过F作DE∥BC,交AB于点D,交AC于点E,若BD+CE=10,则线段DE的长为10.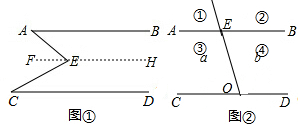 (1)如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,EC.探究∠AEC,∠EAB,∠ECD之间的关系.
(1)如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,EC.探究∠AEC,∠EAB,∠ECD之间的关系.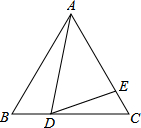 如图,在边长为9的正三角形ABC中,BD=4,∠ADE=60°,则CE的长为$\frac{20}{9}$.
如图,在边长为9的正三角形ABC中,BD=4,∠ADE=60°,则CE的长为$\frac{20}{9}$. 用4块相同的立方体搭成的几何体的主视图如图所示.
用4块相同的立方体搭成的几何体的主视图如图所示. 如图,在△ABC中,AB=AC=5cm,BC=6cm,AD平分∠BAC,则AD=4cm.
如图,在△ABC中,AB=AC=5cm,BC=6cm,AD平分∠BAC,则AD=4cm.