Question

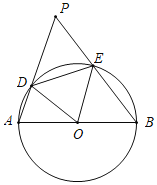
【题目】如图，⊙O中，AB为直径，点P为⊙O外一点，且PA＝AB，PA、PB交⊙O于D、E两点，∠PAB为锐角，连接DE、OD、OE．

（1）求证：∠EDO＝∠EBO；

（2）填空：若AB＝8，

①△AOD的最大面积为　 　；

②当DE＝　 　时，四边形OBED为菱形．

Answer 1

【答案】（1）证明见解析；（2）8；4.

【解析】

（1）如图1，连AE，由等腰三角形的性质可知E为PB中点，则OE是△PAB的中位线，OE∥PA，可证得∠DOE＝∠EOB，则∠EDO＝∠EBO可证；

（2）如图2，由条件知OA＝4，当OA边上的高最大时，△AOD的面积最大，可知点D是的中点时满足题意，此时最大面积为8；

（3）如图3，当DE＝4时，四边形ODEB是菱形．只要证明△ODE是等边三角形即可解决问题．

证明：（1）如图1，连AE，

∵AB为⊙O的直径，

∴∠AEB＝90°，

∵PA＝AB，

∴E为PB的中点，

∵AO＝OB，

∴OE∥PA，

∴∠ADO＝∠DOE，∠A＝∠EOB

∵OD＝OA，

∴∠A＝∠ADO，

∴∠EOB＝∠DOE，

∵OD＝OE＝OB，

∴∠EDO＝∠EBO；

（2）①∵AB＝8，

∴OA＝4，

当OA边上的高最大时，△AOD的面积最大（如图2），此时点D是的中点，

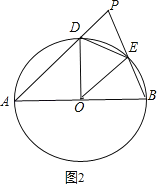
∴OD⊥AB，

∴；

②如图3，当DE＝4时，四边形OBED为菱形，理由如下：

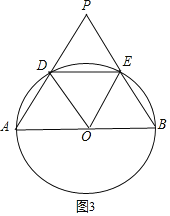
∵OD＝DE＝OE＝4，

∴△ODE是等边三角形，

∴∠EDO＝60°，

由（1）知∠EBO＝∠EDO＝60°，

∴OB＝BE＝OE，

∴四边形OBED为菱形，

故答案为：8；4．