��Ŀ����
����Ŀ����ͼ�٣���ƽ��ֱ������ϵxOy �У�������y=ax2+bx+3������A(-1��0) ��B(3��0) ���㣬����y�ύ�ڵ�C
.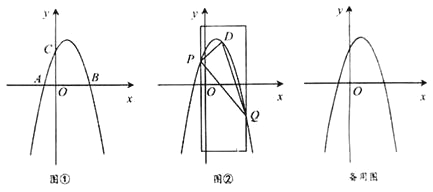
��1���������ߵı���ʽ��
��2����ͼ�ڣ��ÿ�Ϊ4����λ���ȵ�ֱ�ߴ�ֱ��x�ᣬ����x������ƽ�ƣ�ֱ�ߵ������������ڵ�ֱ�����������ཻ��P�� Q���㣨��P�ڵ�Q����ࣩ������PQ�����߶�PQ�Ϸ�����������һ����D������DP��DQ.
������P�ĺ�����Ϊ![]() ������DPQ��������ֵ�������ʱ��D �����ꣻ
������DPQ��������ֵ�������ʱ��D �����ꣻ
��ֱ����ƽ�ƹ����У���DPQ����Ƿ������ֵ�����У������������ֵ����û�У���˵������.
���𰸡���1��������y=-x2+2x+3����2���ٵ�D�� ![]() ��������PQD��������ֵΪ8
��������PQD��������ֵΪ8
����������1�����ݵ�A��B�����꣬���ô���ϵ����������������ߵı���ʽ��
��2����I���ɵ�P�ĺ�����ɵó���P��Q�����꣬���ô���ϵ���������ֱ��PQ�ı���ʽ������D��DE��y�ύֱ��PQ�ڵ�E�����D������Ϊ��x��-x2+2x+3�������E������Ϊ��x��-x+![]() �����������ɵó�DE�ij��ȣ����������ε������ʽ�ɵó�S��DPQ=-2x2+6x+
�����������ɵó�DE�ij��ȣ����������ε������ʽ�ɵó�S��DPQ=-2x2+6x+![]() �������ö��κ��������ʼ��ɽ����ֵ���⣻
�������ö��κ��������ʼ��ɽ����ֵ���⣻
��II��������ڣ����P�ĺ�����Ϊt�����Q�ĺ�����Ϊ4+t�������ɵó���P��Q�����꣬���ô���ϵ���������ֱ��PQ�ı���ʽ�����D������Ϊ��x��-x2+2x+3�������E������Ϊ��x��-2��t+1��x+t2+4t+3�����������ɵó�DE�ij��ȣ����������ε������ʽ�ɵó�S��DPQ=-2x2+4��t+2��x-2t2-8t�������ö��κ��������ʼ��ɽ����ֵ���⣮
��1����A��-1��0����B��3��0������y=ax2+bx+3���ã�
![]() ����ã�
����ã�![]() ��
��
�������ߵı���ʽΪy=-x2+2x+3��
��2����I������P�ĺ�����Ϊ-![]() ʱ����Q�ĺ�����Ϊ
ʱ����Q�ĺ�����Ϊ![]() ��
��
���ʱ��P������Ϊ��-![]() ��
��![]() ������Q��������
������Q��������![]() ��-
��-![]() ����
����
��ֱ��PQ�ı���ʽΪy=mx+n��
��P��-![]() ��
��![]() ����Q��
����Q��![]() ��-
��-![]() ������y=mx+n���ã�
������y=mx+n���ã�
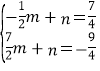 ����ã�
����ã� ��
��
��ֱ��PQ�ı���ʽΪy=-x+![]() ��
��
��ͼ�ڣ�����D��DE��y�ύֱ��PQ�ڵ�E��

���D��������x��-x2+2x+3�������E��������x��-x+![]() ����
����
��DE=-x2+2x+3-��-x+![]() ��=-x2+3x+
��=-x2+3x+![]() ��
��
��S��DPQ=![]() DE��xQ-xP��=-2x2+6x+
DE��xQ-xP��=-2x2+6x+![]() =-2��x-
=-2��x-![]() ��2+8��
��2+8��
��-2��0��
�൱x=![]() ʱ����DPQ�����ȡ���ֵ�����ֵΪ8����ʱ��D������Ϊ��
ʱ����DPQ�����ȡ���ֵ�����ֵΪ8����ʱ��D������Ϊ��![]() ��
��![]() ����
����
��II��������ڣ����P�ĺ�����Ϊt�����Q�ĺ�����Ϊ4+t��
���P��������t��-t2+2t+3������Q��������4+t��-��4+t��2+2��4+t��+3����
���ô���ϵ������֪��ֱ��PQ�ı���ʽΪy=-2��t+1��x+t2+4t+3��
���D��������x��-x2+2x+3�������E��������x��-2��t+1��x+t2+4t+3����
��DE=-x2+2x+3-[-2��t+1��x+t2+4t+3]=-x2+2��t+2��x-t2-4t��
��S��DPQ=![]() DE��xQ-xP��=-2x2+4��t+2��x-2t2-8t=-2[x-��t+2��]2+8��
DE��xQ-xP��=-2x2+4��t+2��x-2t2-8t=-2[x-��t+2��]2+8��
��-2��0��
�൱x=t+2ʱ����DPQ�����ȡ���ֵ�����ֵΪ8��
������������ֱ����ƽ�ƹ����У���DPQ��������ֵ����������ֵΪ8��

����Ŀ��ij������˾��֯20������װ�˼ס��ҡ����������ز���120��ȥ����������ƻ�20������Ҫװ��,ÿ������ֻ��װ��ͬһ�����ز�,�ұ���װ��,�����±��ṩ����Ϣ,�����������
���ز����� | �� | �� | �� |
ÿ������������(��) | 8 | 6 | 5 |
ÿ�����ز�����(��Ԫ) | 12 | 16 | 10 |
(1)��װ�˼������ز��ij�����Ϊx,װ���������ز��ij�����Ϊy,��y��x֮��ĺ�����ϵʽ��
(2)���װ��ÿ�����ز��ij�����������3��,��ô�����İ��ŷ����м���?��д��ÿ�ְ��ŷ�����
(3)��Ҫʹ�˴����ۻ������,Ӧ����(2)�����ְ��ŷ���?�������������ֵ