题目内容
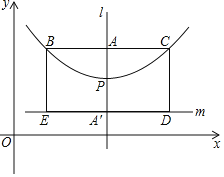
【题目】如图，在顶点为P的抛物线y=a（x-h）2+k（a≠0）的对称轴1的直线上取点A（h，k+
），过A作BC⊥l交抛物线于B、C两点（B在C的左侧），点和点A关于点P对称，过A作直线m⊥l．又分别过点B，C作直线BE⊥m和CD⊥m，垂足为E，D．在这里，我们把点A叫此抛物线的焦点，BC叫此抛物线的直径，矩形BCDE叫此抛物线的焦点矩形．
（1）直接写出抛物线y=
x2的焦点坐标以及直径的长．
（2）求抛物线y=x2-
x+
的焦点坐标以及直径的长．
（3）已知抛物线y=a（x-h）2+k（a≠0）的直径为，求a的值．
（4）①已知抛物线y=a（x-h）2+k（a≠0）的焦点矩形的面积为2，求a的值．
②直接写出抛物线y=x2-x+的焦点短形与抛物线y=x2-2mx+m2+1公共点个数分别是1个以及2个时m的值．
【答案】（1）4（2）4（3）
（4）①a=±
；②当m=1-
或m=5+时，1个公共点，当1-＜m≤1或5≤m＜5+时，2个公共点，
【解析】
（1）根据题意可以求得抛物线y=
x2的焦点坐标以及直径的长；
（2）根据题意可以求得抛物线y=x2-
x+
的焦点坐标以及直径的长；
（3）根据题意和y=a（x-h）2+k（a≠0）的直径为，可以求得a的值；
（4）①根据题意和抛物线y=ax2+bx+c（a≠0）的焦点矩形的面积为2，可以求得a的值；
②根据（2）中的结果和图形可以求得抛物线y=x2-x+的焦点矩形与抛物线y=x2-2mx+m2+1公共点个数分别是1个以及2个时m的值．
（1）∵抛物线y=x2，
∴此抛物线焦点的横坐标是0，纵坐标是：0+
=1，
∴抛物线y=x2的焦点坐标为（0，1），
将y=1代入y=x2，得x1=-2，x2=2，
∴此抛物线的直径是：2-（-2）=4；
（2）∵y=x2-x+=（x-3）2+2，
∴此抛物线的焦点的横坐标是：3，纵坐标是：2+=3，
∴焦点坐标为（3，3），
将y=3代入y=（x-3）2+2，得
3=（x-3）2+2，解得，x1=5，x2=1，
∴此抛物线的直径时5-1=4；
（3）∵焦点A（h，k+
），
∴k+=a（x-h）2+k，解得，x1=h+
，x2=h-，
∴直径为：h+-（h-）=
=，
解得，a=±
，
即a的值是；
（4）①由（3）得，BC=，
又CD=A'A=．
所以，S=BCCD==
=2．
解得，a=±；
②当m=1-或m=5+时，1个公共点，当1-
＜m≤1或5≤m＜5+时，2个公共点，
理由：由（2）知抛，物线y=x2-x+的焦点矩形顶点坐标分别为：
B（1，3），C（5，3），E（1，1），D（5，1），
当y=x2-2mx+m2+1=（x-m）2+1过B（1，3）时，m=1-或m=1+（舍去），过C（5，3）时，m=5-（舍去）或m=5+，
∴当m=1-或m=5+时，1个公共点；
当1-＜m≤1或5≤m＜5+时，2个公共点．
由图可知，公共点个数随m的变化关系为
当m＜1-时，无公共点；
当m=1-时，1个公共点；
当1-＜m≤1时，2个公共点；
当1＜m＜5时，3个公共点；
当5≤m＜5+时，2个公共点；
当m=5+时，1个公共点；
当m＞5+时，无公共点；
由上可得，当m=1-或m=5+时，1个公共点；
当1-＜m≤1或5≤m＜5+时，2个公共点．
