题目内容
19.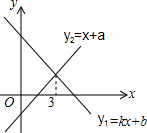 一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③关于x的方程kx-x=a-b的解是x=3;④当x<3时,y1<y2中.则正确的序号有①③.
一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③关于x的方程kx-x=a-b的解是x=3;④当x<3时,y1<y2中.则正确的序号有①③.
分析 根据一次函数的性质对①②进行判断;利用一次函数与一元一次方程的关系对③进行判断;利用函数图象,当x<3时,一次函数y1=kx+b在直线y2=x+a的上方,则可对④进行判断.
解答 解:∵一次函数y1=kx+b经过第一、二、三象限,
∴k<0,b>0,所以①正确;
∵直线y2=x+a的图象与y轴的交点在x轴,下方,
∴a<0,所以②错误;
∵一次函数y1=kx+b与y2=x+a的图象的交点的横坐标为3,
∴x=3时,kx+b=x-a,所以③正确;
当x<3时,y1>y2,所以④错误.
故答案为①③.
点评 本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
7.下列说法正确的是( )
| A. | -(-8)的立方根是-2 | B. | 立方根等于本身数有-1,0,1 | ||
| C. | $-\sqrt{64}$的立方根为-4 | D. | 一个数的立方根不是正数就是负数 |
14.与2$\sqrt{6}$的值最接近的正数是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
4.关于直线l:y=kx+k(k≠0),下列说法中正确的是( )
| A. | 点(0,-k)在直线l上 | B. | y随x的增大而减小 | ||
| C. | 直线l经过第一、二、三象限 | D. | 直线l经过点(-1,0) |
11.有下列命题:①若a>b,则a-b>0;②若a>b>c>0,则ac>bc;③若$\frac{a}{2}$-3>$\frac{b}{2}$-3,则a<b;④若a<b<0,则$\frac{a}{b}$>1.其中真命题有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.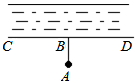 如图,计划把河水引到水池A中,先作AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的数学根据是( )
如图,计划把河水引到水池A中,先作AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的数学根据是( )
 如图,计划把河水引到水池A中,先作AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的数学根据是( )
如图,计划把河水引到水池A中,先作AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的数学根据是( )| A. | 两点之间,线段最短 | |
| B. | 两条平行线之间的距离处处相等 | |
| C. | 经过直线上或直线外一点,有且只有一条直线与已知直线垂直 | |
| D. | 直线外一点与直线上各点连接的所有线段中,垂线段最短 |
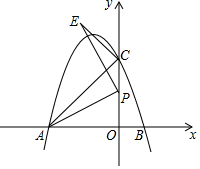 如图,抛物线y=-x2-2x+3与x轴交于A、B两点(A在B的左侧),与y轴交于点C,点P是y轴正半轴上一动点,将点A绕点P顺时针旋转90°得到点E,求证:抛物线的顶点D在直线CE上.
如图,抛物线y=-x2-2x+3与x轴交于A、B两点(A在B的左侧),与y轴交于点C,点P是y轴正半轴上一动点,将点A绕点P顺时针旋转90°得到点E,求证:抛物线的顶点D在直线CE上.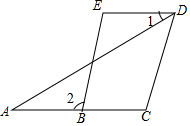 完成下面的证明.
完成下面的证明.