题目内容
11.下列式子一定是二次根式的是( )| A. | $\sqrt{{x}^{2}-2}$ | B. | $\sqrt{-x-2}$ | C. | $\sqrt{x}$ | D. | $\sqrt{{x}^{2}+2}$ |
分析 根据二次根式的被开方数是非负数对每个选项做判断即可.
解答 解:A、当x=±1时,x2-2=-1<0,$\sqrt{{x}^{2}-2}$无意义,此选项错误;
B、当x=1时,-x-2=-3<0,$\sqrt{-x-2}$无意义,此选项错误;
C、当x=-1时,$\sqrt{x}$无意义,此选项错误;
D、∵x2+2≥2,∴$\sqrt{{x}^{2}+2}$符合二次根式定义,此选项正确;
故选:D.
点评 本题考查了二次根式的定义.一般形如$\sqrt{a}$(a≥0)的代数式叫做二次根式.当a≥0时,$\sqrt{a}$表示a的算术平方根;当a小于0时,非二次根式(在一元二次方程中,若根号下为负数,则无实数根.

练习册系列答案
相关题目
19.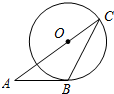 如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连结BC.若∠A=36°,则∠C=( )
如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连结BC.若∠A=36°,则∠C=( )
 如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连结BC.若∠A=36°,则∠C=( )
如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连结BC.若∠A=36°,则∠C=( )| A. | 54° | B. | 36° | C. | 27° | D. | 20° |
6.$\sqrt{16}$的算术平方根是( )
| A. | 4和-4 | B. | 2和-2 | C. | 4 | D. | 2 |
16.已知a+b=5,ab=6,则(a-b)2的值为( )
| A. | 1 | B. | 4 | C. | 9 | D. | 16 |
3. 如图,在正方形ABCD中,点E,F分别在AB,AD上,且BE=AF,连接CE,BF相交于点G,则下列结论不正确的是( )
如图,在正方形ABCD中,点E,F分别在AB,AD上,且BE=AF,连接CE,BF相交于点G,则下列结论不正确的是( )
 如图,在正方形ABCD中,点E,F分别在AB,AD上,且BE=AF,连接CE,BF相交于点G,则下列结论不正确的是( )
如图,在正方形ABCD中,点E,F分别在AB,AD上,且BE=AF,连接CE,BF相交于点G,则下列结论不正确的是( )| A. | BF=CE | B. | ∠AFB=∠ECD | C. | BF⊥CE | D. | ∠AFB+∠BEC=90° |
1.下列二次根式中,属于最简二次根式的是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{0.2}$ | C. | $\sqrt{\frac{1}{2}}$ | D. | $\sqrt{20}$ |
 “瓦当”是中国古代用以装饰美化建筑物檐头的建筑附件,其图案各式各样,属于中国特有的文化艺术遗产.下列“瓦当”的图案中,是轴对称图形的为( )
“瓦当”是中国古代用以装饰美化建筑物檐头的建筑附件,其图案各式各样,属于中国特有的文化艺术遗产.下列“瓦当”的图案中,是轴对称图形的为( )



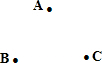 如图,点A,B,C不在同一直线线上.请利用圆规和直尺按下列要求作图(保留作图痕迹,不写作法).
如图,点A,B,C不在同一直线线上.请利用圆规和直尺按下列要求作图(保留作图痕迹,不写作法).