题目内容
12.如图,在平面直角坐标系中,已知点A(3,0),B(0,4),记Rt△OAB为三角形①,按图中所示的方法旋转三角形,依次得到三角形②,③,④,…,则三角形⑤的直角顶点的坐标为($\frac{84}{5}$,$\frac{12}{5}$);三角形⑩的直角顶点的坐标为(36,0);第2015个三角形的直角顶点的坐标为($\frac{40284}{5}$,$\frac{12}{5}$).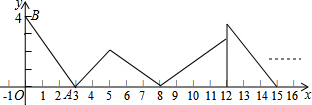
分析 先求出直角三角形斜边上的高,然后根据旋转的性质观察△OAB连续作旋转变换,得到△OAB每三次旋转后回到原来的状态,并且每三次向前移动了3+4+5=12个单位,于是判断三角形的状态,然后可计算出它的直角顶点的横坐标,从而得到三角形⑩的直角顶点的坐标.
解答 解:过点D作DE⊥x轴于点E,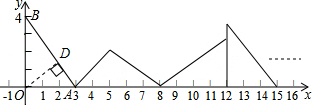
∵点A(3,0),B(0,4),
∴OB=4,OA=3,
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴OD=$\frac{12}{5}$,AD=$\frac{9}{5}$,
三角形①的直角顶点的坐标为(0,0),
三角形②的直角顶点的坐标为(3+$\frac{9}{5}$,$\frac{12}{5}$),
三角形③的直角顶点的坐标为(12,0),
三角形④的直角顶点的坐标为(12,0),
三角形⑤的直角顶点的坐标为(12+3+$\frac{9}{5}$,$\frac{12}{5}$),即($\frac{84}{5}$,$\frac{12}{5}$)
∵对△OAB连续作如图所示的旋转变换,
∴△OAB每三次旋转后回到原来的状态,并且每三次向前移动了3+4+5=12个单位,
而10=3×3+1,
∴三角形⑩和三角形①的状态一样,则三角形⑩与三角形⑨的直角顶点相同
∴三角形⑩的直角顶点的横坐标为3×12=36,纵坐标为0,即(36,0),
∵2015=671×3+2,
∴第2015个三角形和三角形②的状态一样,
则第2015个三角形的直角顶点的横坐标为671×12+3+$\frac{9}{5}$=$\frac{40284}{5}$,纵坐标为$\frac{12}{5}$,
∴第2015个三角形的直角顶点的坐标为($\frac{40284}{5}$,$\frac{12}{5}$).
故答案为:($\frac{84}{5}$,$\frac{12}{5}$),(36,0),($\frac{40284}{5}$,$\frac{12}{5}$).
点评 本题考查了坐标与图形变化-旋转,是对图形变化规律,观察出每三次旋转为一个循环组依次循环,并且下一组的第一个直角三角形与上一组的最后一个直角三角形的直角顶点重合是解题的关键,也是本题的难点.

 _______。
_______。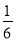 a2b+3a)÷(-
a2b+3a)÷(-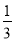 a)=_______
a)=_______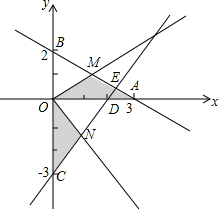 已知直线y=-$\frac{2}{3}$x+2分别与x轴、y轴相交于A、B两点,过点C(0,-3)作直线AB的垂线交直线AB于点E,交x轴于点D.
已知直线y=-$\frac{2}{3}$x+2分别与x轴、y轴相交于A、B两点,过点C(0,-3)作直线AB的垂线交直线AB于点E,交x轴于点D.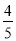 ,求BF的长.
,求BF的长.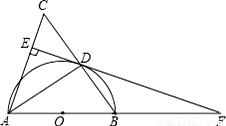
 如图,网格中每个小正方形的边长均为1个单位长度
如图,网格中每个小正方形的边长均为1个单位长度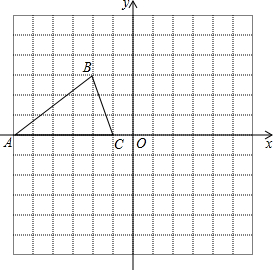 如图,已知△ABC的三个顶点坐标分别为A(-6,0)、B(-2,3)、C(-1,0).
如图,已知△ABC的三个顶点坐标分别为A(-6,0)、B(-2,3)、C(-1,0). 如图,在平面直角坐标系中,△OAB的三个顶点的坐标分别为A(6,3),B(0,5).
如图,在平面直角坐标系中,△OAB的三个顶点的坐标分别为A(6,3),B(0,5).