题目内容
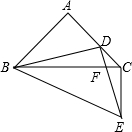如图，Rt△ABC中，∠BAC=90°，AB=AC，AC边上有点D，连接BD，以BD为腰作等腰直角三角形BDE，DE交BC于F，那么下面结论：①△ABD∽△CBE，②∠BCE=90°，③DF•EF=BF•CF，④BC-CE=| 2 |
| A、①② | B、①②③ |
| C、②③④ | D、①②③④ |
考点：相似三角形的判定与性质
专题：
分析：由条件可知△ABC∽△DBE，则可得到
=
，则有
=
，且可得∠ABD=∠CBE，可知①正确，则②也正确，则可证得△DBF∽△CEF，可得到
=
，可得到③，由勾股定理可得BC=
AC，且
=
=
可得CE=
AD，则可得出④，可得出答案．
| AB |
| BD |
| BC |
| BE |
| AB |
| BC |
| BD |
| BE |
| DF |
| CF |
| BF |
| EF |
| 2 |
| AD |
| CE |
| AB |
| BC |
| 1 | ||
|
| 2 |
解答：解：∵△ABC和△DBE为等腰直角三角形，
∴△ABC∽△DBE，
∴
=
，
∴
=
，
∵∠ABD+∠DBC=∠DBC+CBE=45°，
∴∠ABD=∠CBE，
∴△ABD∽△CBE，
∴∠BCE=∠A=90°，
∴①②正确；
在△BDF和△ECF中
∵∠BDE=∠ECF=90°，∠BFD=∠CFE，
∴△BDF∽△ECF，
∴
=
，
∴DF•EF=BF•CF，
∴③正确；
由勾股定理可得BC=
AC，由
=
=
可得CE=
AD，
∴BC-CE=
AC-
AD=
（AC-AD）=
CD，
∴④正确；
综上可知①②③④都正确，
故选D．
∴△ABC∽△DBE，
∴
| AB |
| BD |
| BC |
| BE |
∴
| AB |
| BC |
| BD |
| BE |
∵∠ABD+∠DBC=∠DBC+CBE=45°，
∴∠ABD=∠CBE，
∴△ABD∽△CBE，
∴∠BCE=∠A=90°，
∴①②正确；
在△BDF和△ECF中
∵∠BDE=∠ECF=90°，∠BFD=∠CFE，
∴△BDF∽△ECF，
∴
| DF |
| CF |
| BF |
| EF |
∴DF•EF=BF•CF，
∴③正确；
由勾股定理可得BC=
| 2 |
| AD |
| CE |
| AB |
| BC |
| 1 | ||
|
| 2 |
∴BC-CE=
| 2 |
| 2 |
| 2 |
| 2 |
∴④正确；
综上可知①②③④都正确，
故选D．
点评：本题主要考查相似三角形的判定和性质，证得△ABD∽△CBE是解决其他几个结论的关键，注意利用相似寻找证相似的条件．
练习册系列答案
相关题目
如图所示，一立体图形圆台，它的俯视图是右面的四幅图中的（ ）A、 |
B、 |
C、 |
D、 |
如图，已知一次函数与反比例函数交于点A（-4，-2）和B（a，4），求反比例函数解析式和点B的坐标．
如图，A、B、C为⊙O上三点，且
