题目内容
解答一个问题后,将结论作为条件之一,提出与原问题有关的新问题,我们把它称为原问题的一个“逆向”问题.例如,原问题是“若矩形的两边长分别为3和4,求矩形的周长”,求出周长等于14后,它的一个“逆向”问题可以是“若矩形的周长为14,且一边长为3,求另一边的长”;也可以是“若矩形的周长为14,求矩形面积的最大值”等等.
(1)在矩形ABCD中,对角线AC和BD相交于点O,AB=2,AC=6,求△AOB的周长;
(2)提出(1)的一个“逆向”问题,并解答这个问题.
(1)在矩形ABCD中,对角线AC和BD相交于点O,AB=2,AC=6,求△AOB的周长;
(2)提出(1)的一个“逆向”问题,并解答这个问题.
考点:矩形的性质,命题与定理
专题:开放型
分析:(1)根据矩形的性质:对角线相等且互相平分即可求出△AOB的周长;
(2)根据条件提供的例题和“逆向”的概念解答即可.
(2)根据条件提供的例题和“逆向”的概念解答即可.
解答:解:(1)∵四边形ABCD是矩形,
∴AC=BD,AO=CO=BO=DO,
∴AO=BO=
AC=3,
∵AB=2,
∴△AOB的周长=3+3+2=8;
(2)问题(1)的一个“逆向”问题是:若△AOB的周长是8,AC=6,求AB的长,
解答如下:
∵四边形ABCD是矩形,
∴AC=BD,AO=CO=BO=DO,
∴AO=BO=
AC=3,
∵△AOB的周长是8,
∴AB=8-3-3=2.

∴AC=BD,AO=CO=BO=DO,
∴AO=BO=
| 1 |
| 2 |
∵AB=2,
∴△AOB的周长=3+3+2=8;
(2)问题(1)的一个“逆向”问题是:若△AOB的周长是8,AC=6,求AB的长,
解答如下:
∵四边形ABCD是矩形,
∴AC=BD,AO=CO=BO=DO,
∴AO=BO=
| 1 |
| 2 |
∵△AOB的周长是8,
∴AB=8-3-3=2.
点评:本题属于创新问题,一定要读懂题意,掌握矩形性质,题目比较典型,是一道比较好的题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
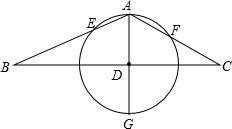 如图,由△ABC的顶点A作高AD,以垂足D为圆心,AD为半径作圆,分别交AB、AC于EF,若AE=2,AF=3,AB=5,求AC的长.
如图,由△ABC的顶点A作高AD,以垂足D为圆心,AD为半径作圆,分别交AB、AC于EF,若AE=2,AF=3,AB=5,求AC的长. 如图,已知一次函数与反比例函数交于点A(-4,-2)和B(a,4),求反比例函数解析式和点B的坐标.
如图,已知一次函数与反比例函数交于点A(-4,-2)和B(a,4),求反比例函数解析式和点B的坐标.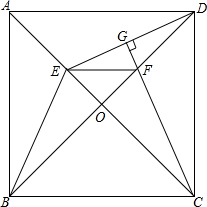 如图,正方形ABCD的对角线AC、BD相交于点O,点E是OA上任意的一点,连接BE、DE.CG⊥DE于点G,交OD于点F,连接EF.求证:四边形EBCF是等腰梯形.
如图,正方形ABCD的对角线AC、BD相交于点O,点E是OA上任意的一点,连接BE、DE.CG⊥DE于点G,交OD于点F,连接EF.求证:四边形EBCF是等腰梯形. 如图,A、B、C为⊙O上三点,且
如图,A、B、C为⊙O上三点,且
 如图,四边形ABEG、GEFH、HFCD都是正方形,请你在图中找出一对相似比不等于1的相似三角形,并说明理由.
如图,四边形ABEG、GEFH、HFCD都是正方形,请你在图中找出一对相似比不等于1的相似三角形,并说明理由.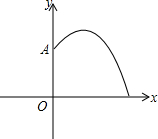 如图是某公园一喷水池,在水池中央有一垂直于地面的喷水柱,喷水时,水流在各方向沿形状相同的抛物线落下.若水流喷出的高度y(m)与水平距离x(m)之间的函数关系式为y=-(x-1)2+2.25
如图是某公园一喷水池,在水池中央有一垂直于地面的喷水柱,喷水时,水流在各方向沿形状相同的抛物线落下.若水流喷出的高度y(m)与水平距离x(m)之间的函数关系式为y=-(x-1)2+2.25