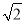题目内容
如图,在等腰△ABC中,AC=BC,分别以AC、BC为边作等边△ACE和△BCD.
(1)当两等边三角形如图(1)所示位置时,BD交AE于F,连接CF,求证:CF平分∠ACB;
(2)都能够两等边三角形如图(2)所示位置时,EA的延长线交DB的延长线于F,(1)中结论是否仍然成立?为什么?
(3)当两等边三角形如图(3)所示位置时,猜想射线CF平分图中的哪些角?(不另作辅助线,不要求证明).
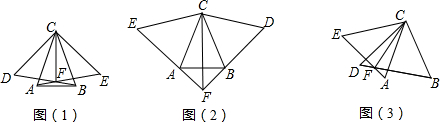
(1)当两等边三角形如图(1)所示位置时,BD交AE于F,连接CF,求证:CF平分∠ACB;
(2)都能够两等边三角形如图(2)所示位置时,EA的延长线交DB的延长线于F,(1)中结论是否仍然成立?为什么?
(3)当两等边三角形如图(3)所示位置时,猜想射线CF平分图中的哪些角?(不另作辅助线,不要求证明).

考点:全等三角形的判定与性质,等腰三角形的性质,等边三角形的性质
专题:
分析:(1)求证△AFC≌△CEB可得∠ACF=∠BCF,得出结论;
(2)结论是否仍然成立,类比(1)的方法求证△AFC≌△CEB可得∠ACF=∠BCF,得出结论;
(3)由(1)(2)可知,实际上CF是整个图形的对称轴所在的直线,由此写出平分的角即可.
(2)结论是否仍然成立,类比(1)的方法求证△AFC≌△CEB可得∠ACF=∠BCF,得出结论;
(3)由(1)(2)可知,实际上CF是整个图形的对称轴所在的直线,由此写出平分的角即可.
解答:
(1)证明:∵CA=CB
∴∠CAB=∠CBA
∵△AEC和△BCD为等边三角形
∴∠CAE=∠CBD,
∴∠FAB=∠FBA
∴AF=BF.
在三角形ACF和△CBF中,
,
∴△AFC≌△CEB(SSS),
∴∠ACF=∠BCF,
∴CF平分∠ACB;
(2)解:结论CF平分∠ACB仍然成立.
理由:∵CA=CB
∴∠CAB=∠CBA
∵△AEC和△BCD为等边三角形
∴∠CAE=∠CBD,
∴∠FAB=∠FBA,
∴AF=BF.
在三角形ACF和△CBF中,
,
∴△AFC≌△CEB(SSS),
∴∠ACF=∠BCF,
∴CF平分∠ACB;
(3)解:CF平分∠ECB,∠ACD,∠EFB,∠DFA.
∴∠CAB=∠CBA
∵△AEC和△BCD为等边三角形
∴∠CAE=∠CBD,
∴∠FAB=∠FBA
∴AF=BF.
在三角形ACF和△CBF中,
|
∴△AFC≌△CEB(SSS),
∴∠ACF=∠BCF,
∴CF平分∠ACB;
(2)解:结论CF平分∠ACB仍然成立.
理由:∵CA=CB
∴∠CAB=∠CBA
∵△AEC和△BCD为等边三角形
∴∠CAE=∠CBD,
∴∠FAB=∠FBA,
∴AF=BF.
在三角形ACF和△CBF中,
|
∴△AFC≌△CEB(SSS),
∴∠ACF=∠BCF,
∴CF平分∠ACB;
(3)解:CF平分∠ECB,∠ACD,∠EFB,∠DFA.
点评:此题考查三角形全等的判定与性质,等边三角形的性质,以及角平分线的意义,结合图形,灵活运用已知条件解决问题.

练习册系列答案
相关题目
下列运算正确的是( )
| A、a4+a5=a9 |
| B、2a4×3a5=6a9 |
| C、a3•a3•a3=3a3 |
| D、(-a3)4=a7 |
已知两个相似三角形的对应中线比为1:3,较大的三角形的周长为18cm,则较小的三角形的周长为( )
| A、6cm | ||
| B、2cm | ||
| C、9cm | ||
D、6
|
下列计算正确的是( )
| A、2x+x=3x2 |
| B、2x2•3x2=6x2 |
| C、x6÷x2=x4 |
| D、2x-x=2 |
下列是二元一次方程的是( )
| A、3x=10 |
| B、2x-3y=-1 |
| C、4x=y-z |
| D、xy+8=0 |
下列计算正确的是( )
| A、7a+a=7a2 |
| B、5y-3y=2 |
| C、3x2y-2x2y=x2y |
| D、3a+2b=5ab |
某人从A地步行到B地,当走到预定时间时,离B地还有0.5千米;若把步行速度提高25%,则可比预定时间早半小时到达B地.已知AB两地相距12.5千米,则某人原来步行的速度是( )
| A、2千米/时 |
| B、4千米/时 |
| C、5千米/时 |
| D、6千米/时 |
下列条件不能判定四边形ABCD是平行四边形的是( )
| A、AB∥CD,AD∥BC |
| B、AD=BC,AB=CD |
| C、AB∥CD,AD=BC |
| D、∠A=∠C,∠B=∠D |
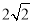 C.2 D.
C.2 D.