题目内容
已知两个相似三角形的对应中线比为1:3,较大的三角形的周长为18cm,则较小的三角形的周长为( )
| A、6cm | ||
| B、2cm | ||
| C、9cm | ||
D、6
|
考点:相似三角形的性质
专题:
分析:利用相似三角形的对应周长比等于相似比,对应中线比等于相似比即可得出.
解答:
解:设较小的三角形的周长为x厘米.则
1:3=x:18,
解得x=6.
故选A.
1:3=x:18,
解得x=6.
故选A.
点评:本题考查对相似三角形性质的理解.利用相似比解题,可使问题简单化.
(1)相似三角形周长的比等于相似比;
(2)相似三角形面积的比等于相似比的平方;
(3)相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比.
(1)相似三角形周长的比等于相似比;
(2)相似三角形面积的比等于相似比的平方;
(3)相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
下列运算正确的是( )
| A、(-2ab)•(-3ab)3=-54a4b4 | ||
| B、5x2•(3x3)2=15x12 | ||
| C、(-0.1 b)•(-10b2)3=-b7 | ||
D、(2×10n)(
|
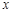 的一元二次方程(a+c)x2+2bx+(a-c)=0,其中a、b、c分别为△ABC三边的长.
的一元二次方程(a+c)x2+2bx+(a-c)=0,其中a、b、c分别为△ABC三边的长.