题目内容
4．
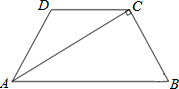如图，在梯形ABCD中，AB∥DC，AD=BC，∠D=120°，AC⊥BC，求tan∠DAC的值．
分析 由在梯形ABCD中，AB∥DC，AD=BC，∠D=120°，首先求得∠B的度数，又由AC⊥BC，可求得∠BAC的度数，继而求得∠DAC的度数，然后由特殊角的三角函数值，求得答案．
解答 解：∵AB∥DC，∠D=120°，
∴∠DAB=180°-∠D=60°，
∵AD=BC，
∴∠C=∠DAB=60°，
∵AC⊥BC，
∴∠BAC=90°-∠D=30°，
∴∠DAC=∠DAB-∠BAC=30°，
∴tan∠DAC=tan30°=$\frac{\sqrt{3}}{3}$．
点评 此题考查了等腰梯形的性质以及特殊角的三角函数问题．注意根据题意求得∠DAC的度数是解此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
14．
如图，在△ABC中，AB=AC，P为△ABC的中线AD上任意一点，若点P到边AB的距离为2cm，则点P到边AC的距离为（ ）
如图，在△ABC中，AB=AC，P为△ABC的中线AD上任意一点，若点P到边AB的距离为2cm，则点P到边AC的距离为（ ）| A． | 1cm | B． | 1.5cm | C． | 2cm | D． | 2.5cm |
15．已知y=（m+1）${x}^{{m}^{2}}$，如果y是x的正比例函数，则m的值为（ ）
| A． | 1 | B． | -1 | C． | 1，-1 | D． | 0 |
12．下列运用等式的性质变形错误的是（ ）
| A． | 若a=b，则a+1=b+1 | B． | 若-3x=-3y，则x=-y | ||
| C． | 若n-2=m-2，则m-n=0 | D． | 若$\frac{a}{2}$=$\frac{b}{2}$，则a=b |
如图，在菱形ABCD中，对角线AC、BD相交于点O，∠BAD=120°，AC=8cm，则菱形ABCD面积是32$\sqrt{3}$ cm2．