题目内容
11. 如图,已知AB∥CD,OA=OD,AE=DF.
如图,已知AB∥CD,OA=OD,AE=DF.(1)求证:OC=OB;
(2)求证:EB∥CF.
分析 (1)由AB∥CD,利用两直线平行得到两对内错角相等,再由OA=OD,利用AAS得到△AOB≌△DOC,利用全等三角形对应边相等得到OC=OB;
(2)由OA+AE=OD+DF求出OF=OE,夹角为对顶角相等,利用SAS得到△COF≌△BOE,利用全等三角形对应角相等得到一对内错角相等,利用内错角相等两直线平行即可得证.
解答 证明:(1)∵AB∥CD,
∴∠DCO=∠ABO,∠CDO=∠BAO,
在△AOB和△DOC中,
$\left\{\begin{array}{l}{∠ABO=∠DCO}\\{∠BAO=∠CDO}\\{OA=OD}\end{array}\right.$,
∴△AOB≌△DOC(AAS),
∴OC=OB;
(2)∵OA=OD,AE=DF,
∴OA+AE=OD+DF,即OA=OF,
在△COF和△BOE中,
$\left\{\begin{array}{l}{OC=OB}\\{∠COF=∠BOE}\\{OF=OE}\end{array}\right.$,
∴△COF≌△BOE(SAS),
∴∠F=∠E,
∴BE∥CF.
点评 此题考查了全等三角形的判定与性质,平行线的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
16.两个数之和为5,其中一个加数是-7,那么另一个加数是( )
| A. | 12 | B. | 2 | C. | -2 | D. | -12 |
 小明家、学校、书店在同-条马路上,请你用学过的数学知识在图中标明它们三者间的距离.小明的步行速度是5千米/时,小明中午11:30放学,下午1:30上课,吃饭要用30分钟,中午他要到书店买完书再到学校上课,选书时间是10分钟.请你帮小明计算一下,他吃完中午饭最晚什么时间从家出发上课才不会迟到?
小明家、学校、书店在同-条马路上,请你用学过的数学知识在图中标明它们三者间的距离.小明的步行速度是5千米/时,小明中午11:30放学,下午1:30上课,吃饭要用30分钟,中午他要到书店买完书再到学校上课,选书时间是10分钟.请你帮小明计算一下,他吃完中午饭最晚什么时间从家出发上课才不会迟到?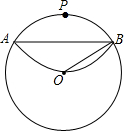 如图,⊙O为一张直径为6的圆形纸片,现将⊙O上任意一点P与圆心O重合折叠,得折痕AB.求折痕AB的长.
如图,⊙O为一张直径为6的圆形纸片,现将⊙O上任意一点P与圆心O重合折叠,得折痕AB.求折痕AB的长. 如图,在△ABC中,∠BAC=90°,AC=2AB,O为AC的中点.AD为高,OG⊥AC,交AD的延长于G,OB交AD于F,OE⊥OB交BC于E.
如图,在△ABC中,∠BAC=90°,AC=2AB,O为AC的中点.AD为高,OG⊥AC,交AD的延长于G,OB交AD于F,OE⊥OB交BC于E. 某小区用14米长的铁栅栏围城一个长方形的花坛,其中一边靠墙,墙长为10米,当AB为多长时,花坛的面积是12平方米?
某小区用14米长的铁栅栏围城一个长方形的花坛,其中一边靠墙,墙长为10米,当AB为多长时,花坛的面积是12平方米?