题目内容
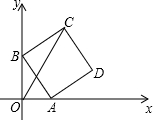 如图,平面直角坐标系中,点A、B分别是x、y轴上的动点,以AB为边作边长为2的正方形ABCD,则OC的最大值为
如图,平面直角坐标系中,点A、B分别是x、y轴上的动点,以AB为边作边长为2的正方形ABCD,则OC的最大值为考点:正方形的性质,三角形三边关系,直角三角形斜边上的中线,勾股定理
专题:
分析:取AB的中点E,连接OE、CE,根据线段中点的定义求出BE,利用勾股定理列式求出CE,再根据直角三角形斜边上的中线等于斜边的一半可得OE=BE,根据两点之间线段最短判断出点O、E、C三点共线时OC最大,然后求解即可.
解答: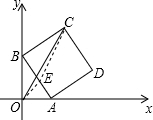 解:如图,取AB的中点E,连接OE、CE,
解:如图,取AB的中点E,连接OE、CE,
则BE=
×2=1,
在Rt△BCE中,由勾股定理得,CE=
=
,
∵∠AOB=90°,点E是AB的中点,
∴OE=BE=1,
由两点之间线段最短可知,点O、E、C三点共线时OC最大,
∴OC的最大值=
+1.
故答案为:
+1.
 解:如图,取AB的中点E,连接OE、CE,
解:如图,取AB的中点E,连接OE、CE,则BE=
| 1 |
| 2 |
在Rt△BCE中,由勾股定理得,CE=
| 22+12 |
| 5 |
∵∠AOB=90°,点E是AB的中点,
∴OE=BE=1,
由两点之间线段最短可知,点O、E、C三点共线时OC最大,
∴OC的最大值=
| 5 |
故答案为:
| 5 |
点评:本题考查了正方形的性质,直角三角形斜边上的中线等于斜边的一半的性质,勾股定理,熟记各性质并确定出OC最大时的情况是解题的关键.

练习册系列答案
相关题目
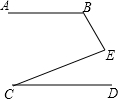 如图,若AB∥CD,则∠B、∠C、∠E三者之间的关系是( )
如图,若AB∥CD,则∠B、∠C、∠E三者之间的关系是( )| A、∠B+∠C+∠E=180° |
| B、∠B+∠E-∠C=180° |
| C、∠B+∠C-∠E=180° |
| D、∠C+∠E-∠B=180° |
 如图,正方形ABCD的边长为a,点E、F分别在边BC、CD上,且∠EAF=45°,求△CEF的周长.
如图,正方形ABCD的边长为a,点E、F分别在边BC、CD上,且∠EAF=45°,求△CEF的周长. 如图,已知AD平分∠BAC交BC于D,CE⊥AD于E,∠B=26°,∠DCE=34°,则∠BAC的度数为
如图,已知AD平分∠BAC交BC于D,CE⊥AD于E,∠B=26°,∠DCE=34°,则∠BAC的度数为