题目内容
 如图,已知AD平分∠BAC交BC于D,CE⊥AD于E,∠B=26°,∠DCE=34°,则∠BAC的度数为
如图,已知AD平分∠BAC交BC于D,CE⊥AD于E,∠B=26°,∠DCE=34°,则∠BAC的度数为考点:三角形内角和定理
专题:
分析:根据三角形的内角和定理可知∠ADC=56°,再根据三角形外角的性质求得∠BAD,再由角平分线即可得出∠BAC的度数.
解答:解:∵CE⊥AD,∠DCE=34°,
∴∠ADC=90°-∠DCE=56°,
∴∠BAD=∠ADC-∠B=30°,
∵AD平分∠BAC,
∴∠BAC=2∠BAD=60°.
∴∠ADC=90°-∠DCE=56°,
∴∠BAD=∠ADC-∠B=30°,
∵AD平分∠BAC,
∴∠BAC=2∠BAD=60°.
点评:此题考查三角形内角和定理,三角形的外角的性质以及角平分线的性质.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
已知某三角形三边分别是m2-n2、2mn、m2+n2(m>n),且m、n都是整数,此三角形是( )
| A、直角三角形 |
| B、等腰直角三角形 |
| C、锐角三角形 |
| D、钝角三角形 |
 小王设计了一“对称跳棋”题:如图,在作业本上画一条直线L,在直线L两边各放一粒围棋子A、B,使线段AB长8cm,并关于直线L对称,在图中P1处有一粒跳棋子,Pl距A点6cm、与直线L的距离为3cm,按以下程序起跳:第1次,从Pl点以A为对称中心跳至P2点;第2次,从P2点以L为对称轴跳至P3点;第3次,从P3点以B为对称中心跳至P4点;第4次,从P4点以L对称轴跳至P5点;….
小王设计了一“对称跳棋”题:如图,在作业本上画一条直线L,在直线L两边各放一粒围棋子A、B,使线段AB长8cm,并关于直线L对称,在图中P1处有一粒跳棋子,Pl距A点6cm、与直线L的距离为3cm,按以下程序起跳:第1次,从Pl点以A为对称中心跳至P2点;第2次,从P2点以L为对称轴跳至P3点;第3次,从P3点以B为对称中心跳至P4点;第4次,从P4点以L对称轴跳至P5点;….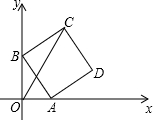 如图,平面直角坐标系中,点A、B分别是x、y轴上的动点,以AB为边作边长为2的正方形ABCD,则OC的最大值为
如图,平面直角坐标系中,点A、B分别是x、y轴上的动点,以AB为边作边长为2的正方形ABCD,则OC的最大值为