题目内容
已知直线l过点A(1,0),B(0,
)两点,将直线l绕点A逆时针旋转90°,交y轴于点C,又知P(m,0).
(1)求直线AB,AC解析式;
(2)求△ABC面积;
(3)若S△ABP=S△ABC,求m的值.
| 3 |
(1)求直线AB,AC解析式;
(2)求△ABC面积;
(3)若S△ABP=S△ABC,求m的值.
考点:一次函数图象与几何变换
专题:
分析:(1)首先设直线AB的解析式为:y=kx+b,由点A(1,0),B(0,
),利用待定系数法即可求得直线AB的解析式;可求得∠BAO的度数,又由直线AB绕点A逆时针旋转90°得到直线AC,即可求得点C的坐标,然后利用待定系数法求得旋转后的直线解析式;
(2)根据△ABC的面积=
•BC•OA,代入计算即可;
(3)设AP=a.先由S△ABP=S△ABC,得出
a•
=
,解方程求出a=
,再由A(1,0),P(m,0),得到|m-1|=
,解方程即可求出m的值.
| 3 |
(2)根据△ABC的面积=
| 1 |
| 2 |
(3)设AP=a.先由S△ABP=S△ABC,得出
| 1 |
| 2 |
| 3 |
2
| ||
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
解答: 解:(1)设直线AB的解析式为:y=kx+b,
解:(1)设直线AB的解析式为:y=kx+b,
∵A(1,0),B(0,
),
∴
,
解得:
,
∴直线AB的解析式为:y=-
x+
;
在Rt△AOB中,∵OA=1,OB=
,
∴tan∠BAO=
=
,
∴∠BAO=60°,
当直线AB绕点A逆时针旋转90°交y轴于点C,
∴∠CAO=90-60°=30°,
在Rt△AOC中,OC=OA•tan30°=1×
=
,
∴点C的坐标为(0,-
),
设所得直线为y=mx-
,
∵A(1,0),
∴0=m-
,
解得:m=
;
∴直线AC解析式为:y=
x-
;
(2)△ABC的面积=
•BC•OA=
×
×1=
;
(3)设AP=a.
∵S△ABP=S△ABC,
∴
a•
=
,
∴a=
.
∵A(1,0),P(m,0),
∴|m-1|=
,
∴m=
或-
.
 解:(1)设直线AB的解析式为:y=kx+b,
解:(1)设直线AB的解析式为:y=kx+b,∵A(1,0),B(0,
| 3 |
∴
|
解得:
|
∴直线AB的解析式为:y=-
| 3 |
| 3 |
在Rt△AOB中,∵OA=1,OB=
| 3 |
∴tan∠BAO=
| OB |
| OA |
| 3 |
∴∠BAO=60°,
当直线AB绕点A逆时针旋转90°交y轴于点C,
∴∠CAO=90-60°=30°,
在Rt△AOC中,OC=OA•tan30°=1×
| ||
| 3 |
| ||
| 3 |
∴点C的坐标为(0,-
| ||
| 3 |
设所得直线为y=mx-
| ||
| 3 |
∵A(1,0),
∴0=m-
| ||
| 3 |
解得:m=
| ||
| 3 |
∴直线AC解析式为:y=
| ||
| 3 |
| ||
| 3 |
(2)△ABC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
4
| ||
| 3 |
2
| ||
| 3 |
(3)设AP=a.
∵S△ABP=S△ABC,
∴
| 1 |
| 2 |
| 3 |
2
| ||
| 3 |
∴a=
| 4 |
| 3 |
∵A(1,0),P(m,0),
∴|m-1|=
| 4 |
| 3 |
∴m=
| 7 |
| 3 |
| 1 |
| 3 |
点评:此题考查了待定系数法求一次函数的解析式、旋转的性质、解直角三角形及三角形的面积.此题难度适中,注意掌握方程思想与数形结合思想的应用.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 如图,A是反比例函数y=
如图,A是反比例函数y=| k |
| x |
| A、-4 | B、1 | C、2 | D、4 |
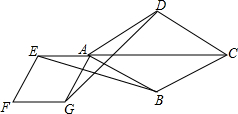 如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,且菱形AEFG∽菱形ABCD,连接EB,GD.
如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,且菱形AEFG∽菱形ABCD,连接EB,GD. 如图,两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.请找出图2中的全等三角形,并给予证明(不再添加其它线段,不再标注或使用其它字母).
如图,两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.请找出图2中的全等三角形,并给予证明(不再添加其它线段,不再标注或使用其它字母).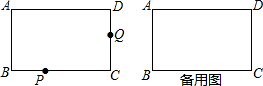
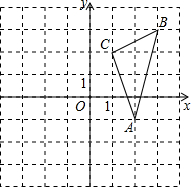 如图,平面直角坐标系中,△ABC的顶点都在网格点上.
如图,平面直角坐标系中,△ABC的顶点都在网格点上.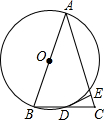 如图,△ABC的边AB为⊙O的直径,BC与圆交于点D,D为BC的中点,过D作DE⊥AC于E.
如图,△ABC的边AB为⊙O的直径,BC与圆交于点D,D为BC的中点,过D作DE⊥AC于E.