题目内容
18.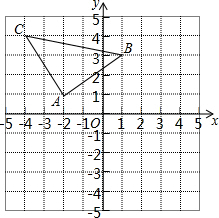 如图,方格纸中每个小正方形的边长都是1个单位长度,建立平面直角坐标系后,△ABC的顶点均在格点上,点A的坐标为(-2,1).
如图,方格纸中每个小正方形的边长都是1个单位长度,建立平面直角坐标系后,△ABC的顶点均在格点上,点A的坐标为(-2,1).(1)作△A1B1C1,使△A1B1C1与△ABC关于y轴对称,并写出点A1的坐标;
(2)△A1B1C1绕原点O顺时针旋转90°得到△A2B2C2,画出△A2B2C2并求出线段B1C1在旋转过程中所扫过的面积.
分析 (1)利用关于y轴对称的性质得出A,B,C对应点坐标,进而得出答案;
(2)利用旋转的性质分别得出对应点位置,进而得出图形,再利用扇形面积求法得出即可.
解答  解:(1)如图所示:△A1B1C1即为所求,点A1的坐标为:(2,1);
解:(1)如图所示:△A1B1C1即为所求,点A1的坐标为:(2,1);
(2)如图所示:△A2B2C2即为所求,
线段B1C1在旋转过程中所扫过的面积为:
S=S△OC1B1+S扇形C1OC2-S扇形B1OB2-S△OC2B2
=S扇形C1OC2-S扇形BOB2
=$\frac{90π×(4\sqrt{2})^{2}}{360}$-$\frac{90π×(\sqrt{10})^{2}}{360}$
=$\frac{11}{2}$π.
点评 此题主要考查了扇形面积公式的应用以及图象的平移和旋转,根据已知得出对应点位置是解题关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
7.在?ABCD中,BD、AC是对角线,下列结论不正确的是( )
| A. | 当AB=BC时,?ABCD是菱形 | B. | 当∠ABC=90°时,?ABCD是矩形 | ||
| C. | 当AC⊥BD时,?ABCD是菱形 | D. | 当AC=BD时,?ABCD是正方形 |
 已知点M(4,0),P(2,y),点N在x轴的负半轴上,且MN=6.
已知点M(4,0),P(2,y),点N在x轴的负半轴上,且MN=6.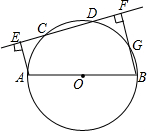 如图所示,AB是⊙O的直径,CD是⊙O的弦,AE⊥CD交直线CD于点E,BF⊥CD交直线CD于点F,若BF交⊙O于G.求证:$\widehat{AC}$=$\widehat{DG}$.
如图所示,AB是⊙O的直径,CD是⊙O的弦,AE⊥CD交直线CD于点E,BF⊥CD交直线CD于点F,若BF交⊙O于G.求证:$\widehat{AC}$=$\widehat{DG}$.