题目内容
15.二次函数y=x2+4x+5中,当x=-2时,y有最小值.分析 先用配方法把函数化为顶点式的形式,再根据其解析式即可求解.
解答 解:∵二次函数y=x2+4x+5可化为y=(x+2)2+1,
∴当x=-2时,二次函数y=x2+4x+5有最小值.
故答案为:-2.
点评 本题考查了二次函数的最值问题,求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
5.如图,用长度相等的小木棒搭成的三角形网格,根据图示填写下列表格.
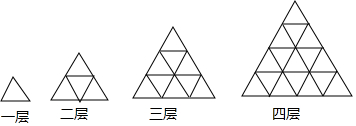

| 层数 | 1 | 2 | 3 | 4 | … | n |
| 所含小三角形的个数 | 1 | 4 | 9 | 16 | … | 4n-3 |
| 所需小木棒的根数 | 3 | 9 | 18 | 30 | … | $\frac{3}{2}$n(n+1) |
3. 如图,△ADC中,∠A=15°,∠D=90°,B在AC的垂直平分线上,AB=34,则CD=( )
如图,△ADC中,∠A=15°,∠D=90°,B在AC的垂直平分线上,AB=34,则CD=( )
 如图,△ADC中,∠A=15°,∠D=90°,B在AC的垂直平分线上,AB=34,则CD=( )
如图,△ADC中,∠A=15°,∠D=90°,B在AC的垂直平分线上,AB=34,则CD=( )| A. | 15 | B. | 17 | C. | 16 | D. | 以上全不对 |
20.已知x、y为正数且$\sqrt{4-{x}^{2}}$+(3-y2)2=0,如果以x,y的长为直角边作一个直角三角形,那么以这个直角三角形的斜边为边长的正方形的面积为( )
| A. | 5 | B. | 25 | C. | 7 | D. | 15 |
7. 如图,点D是△ABC的边AC的上一点,且∠ABD=∠C;如果$\frac{AD}{CD}$=$\frac{1}{3}$,那么$\frac{BD}{BC}$=( )
如图,点D是△ABC的边AC的上一点,且∠ABD=∠C;如果$\frac{AD}{CD}$=$\frac{1}{3}$,那么$\frac{BD}{BC}$=( )
 如图,点D是△ABC的边AC的上一点,且∠ABD=∠C;如果$\frac{AD}{CD}$=$\frac{1}{3}$,那么$\frac{BD}{BC}$=( )
如图,点D是△ABC的边AC的上一点,且∠ABD=∠C;如果$\frac{AD}{CD}$=$\frac{1}{3}$,那么$\frac{BD}{BC}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
5.下面的说法中正确的为( )
| A. | -1不是单项式 | B. | -a表示负数 | ||
| C. | 1是绝对值最小的数 | D. | $x+\frac{1}{x}-1$不是多项式 |
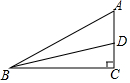 如图,在△ABC 中,∠C=90°,∠ABC的平分线BD交AC于点D,且CD:AD=2:3,AC=15cm,则点D到AB的距离等于6cm.
如图,在△ABC 中,∠C=90°,∠ABC的平分线BD交AC于点D,且CD:AD=2:3,AC=15cm,则点D到AB的距离等于6cm.