题目内容
10.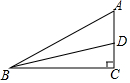 如图,在△ABC 中,∠C=90°,∠ABC的平分线BD交AC于点D,且CD:AD=2:3,AC=15cm,则点D到AB的距离等于6cm.
如图,在△ABC 中,∠C=90°,∠ABC的平分线BD交AC于点D,且CD:AD=2:3,AC=15cm,则点D到AB的距离等于6cm.
分析 过点D作DE⊥AB于E,根据比例求出CD,再根据角平分线上的点到角的两边距离相等可得DE=CD.
解答  解:如图,过点D作DE⊥AB于E,
解:如图,过点D作DE⊥AB于E,
∵AC=15cm,CD:AD=2:3,
∴CD=15×$\frac{2}{5}$=6cm,
∵∠C=90°,BD平分∠ABC,DE⊥AB,
∴DE=CD=6cm,
即点D到AB的距离为6cm.
故答案为:..
点评 本题考查了角平分线上的点到角的两边距离相等的性质,熟记性质是解题的关键.

练习册系列答案
相关题目
1. 有些色彩图案,不仅是轴对称图形,而且颜色也“对称”,如果考虑颜色的“对称”,如图只有一条对称轴,把其中无色小正方形中的两个涂上红色使整个图形是轴对称图形,共有( )种方案.
有些色彩图案,不仅是轴对称图形,而且颜色也“对称”,如果考虑颜色的“对称”,如图只有一条对称轴,把其中无色小正方形中的两个涂上红色使整个图形是轴对称图形,共有( )种方案.
 有些色彩图案,不仅是轴对称图形,而且颜色也“对称”,如果考虑颜色的“对称”,如图只有一条对称轴,把其中无色小正方形中的两个涂上红色使整个图形是轴对称图形,共有( )种方案.
有些色彩图案,不仅是轴对称图形,而且颜色也“对称”,如果考虑颜色的“对称”,如图只有一条对称轴,把其中无色小正方形中的两个涂上红色使整个图形是轴对称图形,共有( )种方案.| A. | 4 | B. | 5 | C. | 6 | D. | 多于6 |
2.在-$\frac{1}{2}$,-|12|,-20,0,-(-5)中,负数的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
19.已知ab>0,则$\frac{a}{|a|}$+$\frac{|b|}{b}$+$\frac{ab}{|ab|}$=( )
| A. | 3 | B. | -3 | C. | 3或-1 | D. | 3或-3 |
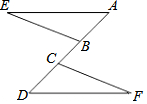 如图,已知A、B、C、D在一条直线上,EB=FC,EB∥FC,∠E=∠F,试说明:
如图,已知A、B、C、D在一条直线上,EB=FC,EB∥FC,∠E=∠F,试说明: 如图,点B、D、F在AN上,C、E在AM 上,且AB=BC=CD=ED=EF,∠A=20°,则∠FEB=70度.
如图,点B、D、F在AN上,C、E在AM 上,且AB=BC=CD=ED=EF,∠A=20°,则∠FEB=70度. 如图,一个无盖的圆柱纸盒:高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是10cm.
如图,一个无盖的圆柱纸盒:高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是10cm.