题目内容
16.解不等式组,并把解集在数轴上表示出来:-1$<\frac{3-2x}{2}$≤2.分析 先根据题意得出关于x的不等式组,求出x的取值范围,再在数轴上表示出来即可.
解答 解:由题意得,$\left\{\begin{array}{l}\frac{3-2x}{2}>-1①\\ \frac{3-2x}{2}≤2②\end{array}\right.$,
由①得,x<$\frac{5}{2}$,
由②得,x≥-$\frac{5}{2}$,
故不等式组的解集为:-$\frac{5}{2}$≤x<$\frac{5}{2}$.
在数轴上表示为: .
.
点评 本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.若3a=27,3b=9,则3b-a=( )
| A. | 3 | B. | 18 | C. | $\frac{1}{3}$ | D. | 36 |
11.若李玲从学校出发先向东走1000米,再向南走1500米便可到家,则用(1000,-1500)表示李玲家的位置,若王辉从学校出发先向西走500米,再向北走2000米便可到家,则用(-500,2000)表示王辉家的位置,若刘晓从学校出发先向东走1500米,再向北走1500米便可到家,则刘晓家的位置可表示为( )
| A. | (1500,1500) | B. | (-1500,1500) | C. | (1500,-1500) | D. | (-1500,-1500) |
5.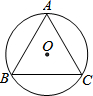 如图,⊙O是等边三角形ABC的外接圆,⊙O的半径为2,则等边△ABC的边长为( )
如图,⊙O是等边三角形ABC的外接圆,⊙O的半径为2,则等边△ABC的边长为( )
 如图,⊙O是等边三角形ABC的外接圆,⊙O的半径为2,则等边△ABC的边长为( )
如图,⊙O是等边三角形ABC的外接圆,⊙O的半径为2,则等边△ABC的边长为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
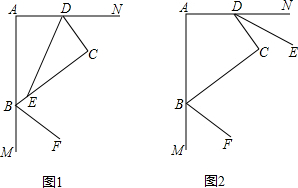
 如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可供利用25m),现在已备足可以砌50m长的墙的材料.
如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可供利用25m),现在已备足可以砌50m长的墙的材料.