题目内容
15.函数y=$\frac{k}{x}$的图象位于第一、三象限,则一次函数y=kx+k的图象不经过第四象限.分析 根据反比例函数的性质可以确定k的符号,再根据一次函数的性质即可解答.
解答 解:∵反比例函数y=$\frac{k}{x}$图象在一、三象限,
∴k>0,
则一次函数y=kx+k图象经过一、二、三象限,不经过第四象限.
故答案为:四.
点评 本题考查了一次函数的图象与系数的关系及反比例函数的性质的知识,反比例函数的性质:
(1)当k>0时,图象分别位于第一、三象限;当k<0时,图象分别位于第二、四象限;
(2)当k>0时,在同一个象限内,y随x的增大而减小;当k<0时,在同一个象限,y随x的增大而增大

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
6.如图四个几何体:其中从左面看到的形状图与从上面看到的形状图相同的几何体共有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.下列各组数中不能作为直角三角形的三边长的是( )
| A. | 6,8,10 | B. | 7,24,25 | C. | 1.5,2,3 | D. | 9,12,15 |
7.按要求完成下列各题.
(1)计算:(-8)-(-$\frac{5}{2}$)+$\frac{1}{4}$-10
(2)比较下列两个数的大小:-$\frac{1}{6}$和-$\frac{1}{7}$.
(1)计算:(-8)-(-$\frac{5}{2}$)+$\frac{1}{4}$-10
(2)比较下列两个数的大小:-$\frac{1}{6}$和-$\frac{1}{7}$.
2.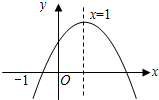 二次函数y=ax2+bx+c图所示,其中正确的结论是( )
二次函数y=ax2+bx+c图所示,其中正确的结论是( )
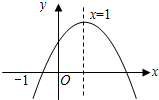 二次函数y=ax2+bx+c图所示,其中正确的结论是( )
二次函数y=ax2+bx+c图所示,其中正确的结论是( )| A. | b2-4ac<0 | B. | abc>0 | C. | 2a+b=0 | D. | a+b+c<0 |
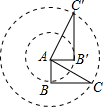 如图,Rt△ABC中,AC=$\sqrt{5}$,以点A为中心逆时针旋转90°得到Rt△AB′C′,则Rt△A′B′C′,则$\widehat{CC′}$的长为$\frac{\sqrt{5}}{2}$π.
如图,Rt△ABC中,AC=$\sqrt{5}$,以点A为中心逆时针旋转90°得到Rt△AB′C′,则Rt△A′B′C′,则$\widehat{CC′}$的长为$\frac{\sqrt{5}}{2}$π. 二次函数y=ax2+bx+c的图象如图所示,则b>0,b2-4ac>0,a-b+c<0.
二次函数y=ax2+bx+c的图象如图所示,则b>0,b2-4ac>0,a-b+c<0.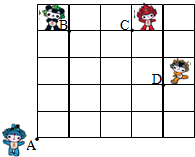 如图,奥运福娃在5×5的方格(每小格边长为1m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其它福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中,
如图,奥运福娃在5×5的方格(每小格边长为1m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其它福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中,