题目内容
20.已知y关于x的二次函数y=(k-1)x2-2kx+k+2的图象与x轴有交点,则k的取值范围是k≤2且k≠1.分析 令y=(k-1)x2-2kx+k+2=0,当判别式△=b2-4ac≥0时,抛物线y=(k-1)x2-2kx+k+2与x轴有交点,再根据k-1≠0,求k的取值范围.
解答 解:由于函数y=(k-1)x2-2kx+k+2的图象与x轴有交点,
则令y=0,则(k-1)x2-2kx+k+2=0,则
△=4k2-4(k-1)(k+2)≥0,且k-1≠0,
解得,k≤2且k≠1.
故答案为:k≤2且k≠1.
点评 本题考查了抛物线与x轴的交点.二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系.△=b2-4ac决定抛物线与x轴的交点个数.△=b2-4ac>0时,抛物线与x轴有2个交点;
△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
11.如图,自行车每节链条的长度为2.5cm,交叉重叠部分的圆的直径为0.8cm.
(1)观察图形填写下表:
(2)如果x节链条的总长度是y,求y与x之间的关系式;
(3)如果一辆某种型号自行车的链条(安装前)由80节这样的链条组成,那么这根链条完成链接(安装到自行车上)后,总长度是多少cm?

(1)观察图形填写下表:
| 链条节数(节) | 2 | 3 | 4 |
| 链条长度(cm) | 4.2 | 5.9 | 7.6 |
(3)如果一辆某种型号自行车的链条(安装前)由80节这样的链条组成,那么这根链条完成链接(安装到自行车上)后,总长度是多少cm?

8.在0,1,-2,3这四个数中,最小的数是( )
| A. | -2 | B. | 1 | C. | 0 | D. | 3 |
15.学校最近新配备了一批图书需要甲乙两人进行整理,若甲单独整理完成需要4小时完工;若甲乙共同整理2小时后,乙再单独整理2小时才能完工,则乙单独整理完成需要( )
| A. | 4小时 | B. | 6小时 | C. | 8小时 | D. | 10小时 |
12.下列图形中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
9.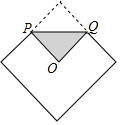 将边长为1的正方形巾的一角折叠至正方形的中心位置,折痕PQ的长为( )
将边长为1的正方形巾的一角折叠至正方形的中心位置,折痕PQ的长为( )
 将边长为1的正方形巾的一角折叠至正方形的中心位置,折痕PQ的长为( )
将边长为1的正方形巾的一角折叠至正方形的中心位置,折痕PQ的长为( )| A. | 1 | B. | 2 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
 如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论是①②③④⑤.
如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论是①②③④⑤.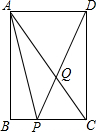 如图,矩形ABCD中,AB=4,AD=3,点Q在对角线AC上,且AQ=AD,连接DQ并延长,与边BC交于点P,则线段AP=$\sqrt{17}$.
如图,矩形ABCD中,AB=4,AD=3,点Q在对角线AC上,且AQ=AD,连接DQ并延长,与边BC交于点P,则线段AP=$\sqrt{17}$.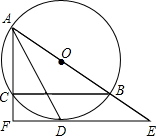 如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的直线分别交AB,AC的延长线于点E,F,AF⊥EF.
如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的直线分别交AB,AC的延长线于点E,F,AF⊥EF.