题目内容
已知,AC,BD相交于点O,BP,CP分别平分∠ABD,∠ACD交于点P.
(1)若∠A=70°,∠D=60°,求∠P的度数;
(2)试探索∠P与∠A、∠D间的数量关系;
(3)若∠A:∠D:∠P=2:4:x,求x的值.
(1)若∠A=70°,∠D=60°,求∠P的度数;
(2)试探索∠P与∠A、∠D间的数量关系;
(3)若∠A:∠D:∠P=2:4:x,求x的值.
考点:对顶角、邻补角,角平分线的定义
专题:
分析:(1)运用三角形的外角等于两个不相邻的内角的和,可得∠D+∠DCN=∠P+∠PBN,∠A+∠ABP=∠P+∠ACP,再根据角平分线的定义和等式的性质可得∠D+∠A=2∠P,从而求出∠P的度数;
(2)由(1)可求得∠P=
(∠A+∠D);
(3)代入(2)的关系式可求得x的值.
(2)由(1)可求得∠P=
| 1 |
| 2 |
(3)代入(2)的关系式可求得x的值.
解答:
解:(1)∵∠BNC=∠D+∠DCN,∠BNC=∠P+∠PBN(三角形的外角等于两个不相邻的内角的和),
∴∠D+∠DCN=∠P+∠EBN(等量代换),
同理:∠A+∠ABP=∠P+∠ACP,
∴∠D+∠DCN+∠A+∠ABP=2∠P+∠PBN+∠ACP(等式性质),
∵BP,CP分别平分∠ABD,∠ACD,
∴∠DCN=∠ACP,∠ABP=∠PBN(角平分线的定义),
∴∠D+∠A=2∠P(等式性质),
∵∠A=70°,∠D=60°,
∴∠P=65°;
(2)由(1)可得∠D+∠A=2∠P,即∠P=
(∠A+∠D);
(3)由∠A:∠D:∠P=2:4:x,可设∠A=2k,∠D=4k,∠P=xk(k≠0),代入∠D+∠A=2∠P可得:6k=2xk,解得x=3.

解:(1)∵∠BNC=∠D+∠DCN,∠BNC=∠P+∠PBN(三角形的外角等于两个不相邻的内角的和),
∴∠D+∠DCN=∠P+∠EBN(等量代换),
同理:∠A+∠ABP=∠P+∠ACP,
∴∠D+∠DCN+∠A+∠ABP=2∠P+∠PBN+∠ACP(等式性质),
∵BP,CP分别平分∠ABD,∠ACD,
∴∠DCN=∠ACP,∠ABP=∠PBN(角平分线的定义),
∴∠D+∠A=2∠P(等式性质),
∵∠A=70°,∠D=60°,
∴∠P=65°;
(2)由(1)可得∠D+∠A=2∠P,即∠P=
| 1 |
| 2 |
(3)由∠A:∠D:∠P=2:4:x,可设∠A=2k,∠D=4k,∠P=xk(k≠0),代入∠D+∠A=2∠P可得:6k=2xk,解得x=3.
点评:本题主要考查三角形外角的性质,解题的关键是在复杂图形中观察出外角和内角之间的关系,有一定的难度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
对于二次函数y=(a2+3)x2,下列命题中正确的是( )
| A、函数图象开口方向不确定 |
| B、当a<0时,函数图象向下开口 |
| C、此抛物线的对称轴是y轴 |
| D、当x<0时,y随x的增大而增大 |
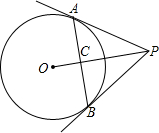 如图,PA,PB分别切圆O于点A,B,圆O的半径为
如图,PA,PB分别切圆O于点A,B,圆O的半径为