题目内容
5.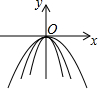 如图所示,在同一平面直角坐标系中,作出①y=-3x2,②y=-$\frac{1}{2}{x}^{2}$,③y=-x2的图象,则从里到外的三条抛物线对应的函数依次是①③②(填序号)
如图所示,在同一平面直角坐标系中,作出①y=-3x2,②y=-$\frac{1}{2}{x}^{2}$,③y=-x2的图象,则从里到外的三条抛物线对应的函数依次是①③②(填序号)
分析 抛物线的形状与|a|有关,根据|a|的大小即可确定抛物线的开口的宽窄.
解答 解:①y=-3x2,
②y=-$\frac{1}{2}$x2,
③y=-x2中,二次项系数a分别为-3、-$\frac{1}{2}$、-1,
∵|-3|>|-1|>|-$\frac{1}{2}$|,
∴抛物线②y=-$\frac{1}{2}$x2的开口最宽,抛物线①y=-3x2的开口最窄.
故答案为:①③②.
点评 本题考查了二次函数的图象,抛物线的开口大小由|a|决定,|a|越大,抛物线的开口越窄;|a|越小,抛物线的开口越宽.

练习册系列答案
相关题目
10.下列命题错误的是( )
| A. | 两个相似三角形的对应角相等,对应值成比例 | |
| B. | 两个全等三角形一定相似 | |
| C. | 两个等腰三角形一定是相似 | |
| D. | 相似的两个三角形不一定全等 |
15.某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用含x的代数式来表示销售量(件)和销售该品牌玩具获得利润(元),并把化简后的结果填写在表格中:
(2)在(1)问条件下,若商场获得了10000元销售利润,试问该玩具销售单价x应定为多少元?
(3)在(1)问条件下,商场有可能获得13000元的销售利润吗?若可能,请求出该玩具销售单价;若不可能,请说明理由.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用含x的代数式来表示销售量(件)和销售该品牌玩具获得利润(元),并把化简后的结果填写在表格中:
| 销售单价(元) | x |
| 销售量(件) | 1000-10x |
| 销售玩具获得利润(元) | -10x2+1300x-30000 |
(3)在(1)问条件下,商场有可能获得13000元的销售利润吗?若可能,请求出该玩具销售单价;若不可能,请说明理由.
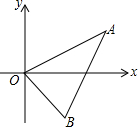 如图,已知A (4,2),B(2,-2),以点O为位似中心,按位似比1:2把△ABO缩小,则点A的对应点A′的坐标为(2,1)或(-2,-1).
如图,已知A (4,2),B(2,-2),以点O为位似中心,按位似比1:2把△ABO缩小,则点A的对应点A′的坐标为(2,1)或(-2,-1).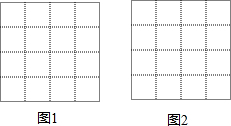 在图1、图2中的每个小正方形的边长都是1.
在图1、图2中的每个小正方形的边长都是1.