题目内容
若圆的内接正多边形的边长是边心距的
倍,求这个正多边形的中心角的度数.
| 2 |
| 3 |
| 3 |
考点:正多边形和圆
专题:
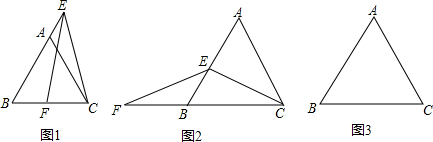
分析:如图,作辅助线,首先证明∠AOC=∠BOC,求出∠AOC的度数,进而求出∠AOB的度数,问题即可解决.
解答: 解:如图,连接OA、OB;AB为⊙O的内接正多边形的一边,
解:如图,连接OA、OB;AB为⊙O的内接正多边形的一边,
OC⊥AB于点C,且AB=
OC;
则AC=BC=
AB=
OC;
∵OA=OB,
∴∠AOC=∠BOC=
∠AOB;
∵tan∠AOC=
=
,
∴∠AOC=30°,
∴∠AOB=60°,
即这个正多边形的中心角为60°.
 解:如图,连接OA、OB;AB为⊙O的内接正多边形的一边,
解:如图,连接OA、OB;AB为⊙O的内接正多边形的一边,OC⊥AB于点C,且AB=
2
| ||
| 3 |
则AC=BC=
| 1 |
| 2 |
| ||
| 3 |
∵OA=OB,
∴∠AOC=∠BOC=
| 1 |
| 2 |
∵tan∠AOC=
| AC |
| OC |
| ||
| 3 |
∴∠AOC=30°,
∴∠AOB=60°,
即这个正多边形的中心角为60°.
点评:该题以圆内接正多边形为载体,以考查垂径定理、直角三角形的边角关系等知识点为核心构造而成;解题的关键是作辅助线,灵活运用有关定理来分析、解答.

练习册系列答案
相关题目
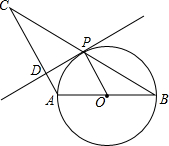 如图,△ABC中,AB=AC,以AB为直径的圆O交BC于点P,PD⊥AC于点D
如图,△ABC中,AB=AC,以AB为直径的圆O交BC于点P,PD⊥AC于点D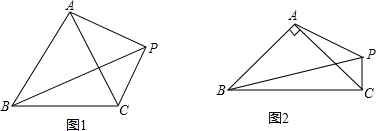
 如图,在角坐标系中,射线Ox绕原点O逆时针旋转300°到OP的位置,若OP=2,则点P的坐标为
如图,在角坐标系中,射线Ox绕原点O逆时针旋转300°到OP的位置,若OP=2,则点P的坐标为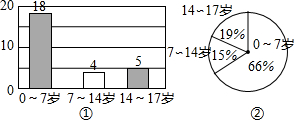 小明、小亮和小丽想要了解他们所生活的小区里小朋友的年龄情况,小明调查了当天在院子里玩耍的小朋友,调查情况如图①所示;小亮调查了他所居住的二单元的小朋友,情况如图②所示;小丽调查了每个单元一楼的两家住户中小朋友的年龄,数据如下(单位:岁):3、16、14、15、17、8、4、6、9、7、17、12、2、13、6、5、12、14、3、15、5、16、1、1.
小明、小亮和小丽想要了解他们所生活的小区里小朋友的年龄情况,小明调查了当天在院子里玩耍的小朋友,调查情况如图①所示;小亮调查了他所居住的二单元的小朋友,情况如图②所示;小丽调查了每个单元一楼的两家住户中小朋友的年龄,数据如下(单位:岁):3、16、14、15、17、8、4、6、9、7、17、12、2、13、6、5、12、14、3、15、5、16、1、1. 已知:线段AB=3.
已知:线段AB=3.