题目内容
一个纸盒内有4张完全相同的卡片,分别标号为1,2,3,4.随机抽取一张卡片后不放回,再随机抽取另一张卡片.
(1)用列举法求“两次抽出卡片的标号等于5”的概率;
(2)小明同学连续做了9次试验,这9次试验没有一次出现“两次抽出卡片的标号和等于5”.他说,“第10次试验我一定能够‘两次抽出卡片的标号和等于5’”.你认为他说得对吗,为什么?
(1)用列举法求“两次抽出卡片的标号等于5”的概率;
(2)小明同学连续做了9次试验,这9次试验没有一次出现“两次抽出卡片的标号和等于5”.他说,“第10次试验我一定能够‘两次抽出卡片的标号和等于5’”.你认为他说得对吗,为什么?
考点:列表法与树状图法,概率的意义
专题:
分析:(1)依据题意先用列表法或画树状图法分析所有等可能的出现结果,然后根据概率公式求出该事件的概率;
(2)根据概率的意义回答即可.
(2)根据概率的意义回答即可.
解答:解:(1)解法一:列表
∴P(和为5)=
=
;
方法二:画树状图:

∴P(和为5)=
=
;
(2)小明说法错误;
因为尽管前9次试验没有一次出现“两次抽出卡片的标号和等于5”,但是第10次试验出现‘两次抽出卡片的标号和等于5”的概率仍为
,
所以小明说法错误.
| 1 | 2 | 3 | 4 | |
| 1 | 1,2 | 1,3 | 1,4 | |
| 2 | 2,1 | 2,3 | 2,4 | |
| 3 | 3,1 | 3,2 | 3,4 | |
| 4 | 4,1 | 4,2 | 4,3 |
| 4 |
| 12 |
| 1 |
| 3 |
方法二:画树状图:

∴P(和为5)=
| 4 |
| 12 |
| 1 |
| 3 |
(2)小明说法错误;
因为尽管前9次试验没有一次出现“两次抽出卡片的标号和等于5”,但是第10次试验出现‘两次抽出卡片的标号和等于5”的概率仍为
| 1 |
| 3 |
所以小明说法错误.
点评:考查概率的求法;得到所求的情况数的解决本题的关键;用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知:如图,在矩形ABCD中,点E在CD上,BF⊥AE,垂足为F,AE2=AD•AB.求证:AE=BF.
已知:如图,在矩形ABCD中,点E在CD上,BF⊥AE,垂足为F,AE2=AD•AB.求证:AE=BF.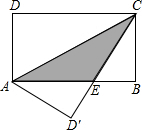 如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,CD落在AB上的点为E点,则重叠部分△AEC的面积是多少?
如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,CD落在AB上的点为E点,则重叠部分△AEC的面积是多少? 如图,在等腰三角形ABC中,AB=AC,两底角的平分线BE、CD相交于点O.
如图,在等腰三角形ABC中,AB=AC,两底角的平分线BE、CD相交于点O.